Question 880687: A three-letter code is generated using the letters of the alphabet. How many of these codes contain at least 1 vowel? The answer is apparently 7620. Does order matter? Are repetitions allowed?
This is what I have tried so far:
At least 1 vowel means that the 3 letter code can either contain 1 vowel, 2 vowels, or 3 vowels so I set up my equation like this:
(5C1 * 21C2) + (5C2 * 21C1) + (5C3 * 21C0) = 1270
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! You used combinations rather than permutations;
so you are finding the number of sets (order does not matter) of 3 letters including at least one vowel, no repetitions allowed.
One of your sets is {A,B,C}.
However, the set {A,B,C} is shared by  different codes.
Codes ABC, ACB, BAC, BCA, CAB, and CBA are considered different codes, because they are different permutations of the elements of the set, and for a code order matters.
Each of your 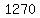 sets of 3 letters generates  codes,
and  .
The result 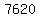 requires that it be specified that repetitions are not allowed. (If repetitions were allowed, as usually happens for codes< the result would be a higher number, but the problem would not be so interesting).
That result 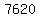can be reached most directly by
subtracting the number of 3-consonant no-repeat codes,  ,
from the number of 3-letter no-repeat codes,  .
|
|
|
