SOLUTION: How many combinations of four letters each can be made from the word pepper? Thanks.

Algebra ->  Permutations -> SOLUTION: How many combinations of four letters each can be made from the word pepper? Thanks.      Log On


   

Question 880670: How many combinations of four letters each can be made from the
word pepper?
Thanks.
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
If you could tell the p's apart and the e's apart, the answer would be 6!.  But
since we can't, the 6! counts the same arrangement too many times, so we must
divide by the number of ways the 3 p's can be rearranged and also by the number
of ways the 2 e's can be rearranged so, we must divide by 3!×2!

Answer 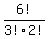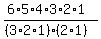6%21%2F3%212%21 = %286%2A5%2A4%2A3%2A2%2A1%29%2F%28%283%2A2%2A1%29%282%2A1%29%29.  After cancelling and multiplying, you get 60.

You didn't ask for them, but here they all are in alphabetical order:

 1. eepppr
 2. eepprp
 3. eeprpp
 4. eerppp
 5. epeppr
 6. epeprp
 7. eperpp
 8. eppepr
 9. epperp
10. eppper
11. epppre
12. epprep
13. epprpe
14. eprepp
15. eprpep
16. eprppe
17. ereppp
18. erpepp
19. erppep
20. erpppe
21. peeppr
22. peeprp
23. peerpp
24. pepepr
25. peperp
26. pepper  <--- the original word
27. peppre
28. peprep
29. peprpe
30. perepp
31. perpep
32. perppe
33. ppeepr
34. ppeerp
35. ppeper
36. ppepre
37. pperep
38. pperpe
39. pppeer
40. pppere
41. pppree
42. ppreep
43. pprepe
44. pprpee
45. preepp
46. prepep
47. preppe
48. prpeep
49. prpepe
50. prppee
51. reeppp
52. repepp
53. reppep
54. repppe
55. rpeepp
56. rpepep
57. rpeppe
58. rppeep
59. rppepe
60. rpppee

Edwin