Question 865065: A typical Social Security number is 555-47-5593. How many Social Security numbers are possible if the first two digits cannot be 0?
Found 2 solutions by jim_thompson5910, richwmiller:
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! "the first two digits cannot be 0", but they can be any number in the set {1,2,3,4,5,6,7,8,9}
So you have 9 choices for the first two slots. The remaining 7 slots have 10 choices (0 through 9) since 0 is allowed
So you just multiply all the choices for each slot (this is the counting principle in action)
9*9*10*10*10*10*10*10*10 = 810,000,000
as a shortcut you can compute 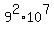 to get the same answer.
-------------------------------------------------------
Final Answer: 810,000,000
Note: this is the number 810 million
Another Note: In scientific notation, the answer is  Scientific notation is often used for really really large numbers.
Answer by richwmiller(17219)  (Show Source):
|
|
|
