SOLUTION: how many different arrangement of the letters in the word "ellipses" can be formed if the consonants must be together?

"ellipses" has consonants l,l,p,s,s and vowels e,i,e

First we find the number of ways positions can be chosen
to make sure the 5 consonants are together:

There are the following 4 ways of choosing positions 1 through 8
to be held by consonants and vowels.  There are these four with 
the 5 consonants together:
 
CCCCCVVV, VCCCCCVV, VVCCCCCV, and VVVCCCCC

For each of those 4 choices of positions to be held by 
consonants and vowels,

there are 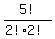 = 30  ways to arrange the consonants since the
2 l's are indistinguishable and the two s's are indistinguishable,

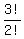and there are  = 3 ways to arrange the vowels since the 2 e's
are indistinguishable.

Answer 4×30×3 = 360 

Edwin