SOLUTION: There are 8 black balls and 5 red balls in an urn. If 5 balls are drawn without replacement, what is the probability that exactly 1 black ball is drawn?

Algebra ->  Permutations -> SOLUTION: There are 8 black balls and 5 red balls in an urn. If 5 balls are drawn without replacement, what is the probability that exactly 1 black ball is drawn?      Log On


   

Question 857413: There are 8 black balls and 5 red balls in an urn. If 5 balls are drawn without replacement, what is the probability that exactly 1 black ball is drawn?
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
To get the numerator of the probability:

Choose the 1 black ball any of C(8,1) ways.
Choose the other four red balls C(5,4) ways

That's C(8,1)×C(5,4) = 8×5 = 40 ways.

To get the denominator:
Choose any 5 balls from the 13 in C(13,5) = 1287 ways.

Probability that exactly 1 black ball is drawn = 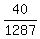40%2F1287,
approximately 3.1% of the time.

Edwin