Question 849902: Digits a, b, and c can be chosen to make the following
multiplication work. What is the 3-digit number abc.
a b c
× 2 4
1 c b a 2
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
You can put this solution on YOUR website! Digits a, b, and c can be chosen to make the following
multiplication work. What is the 3-digit number abc.
a b c
× 2 4
1 c b a 2
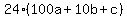  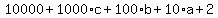 It's obvious that c must be either 8 or 3, since 8x4=32 and 4x3=12,
the only ways to get a last digit of 2.
We try c=8
It's obvious that c must be either 8 or 3, since 8x4=32 and 4x3=12,
the only ways to get a last digit of 2.
We try c=8
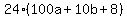  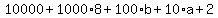 Simplify
Simplify
  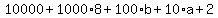
  
  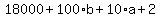
  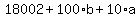
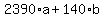  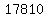 Divide through by 10
Divide through by 10
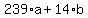  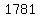 Even if a and b were both the greatest possible digits, which
is 9, the left side would be only 23*9+14*9 = 333, far short
of 1781. Thus we have ruled out c=8 as possible. So c=3
Even if a and b were both the greatest possible digits, which
is 9, the left side would be only 23*9+14*9 = 333, far short
of 1781. Thus we have ruled out c=8 as possible. So c=3
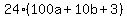  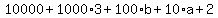 Simplify:
Simplify:
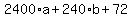  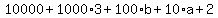
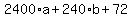  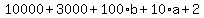
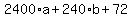  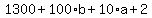
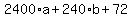  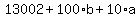
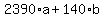   Divide through by 10
Divide through by 10
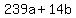  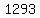 We solve this Diophantine equation:
Since 14 is the coefficient with the smallest
absolute value, 14, we write the 239 and the
1293 in terms of their closest multiple of 14.
239/14 = 17.071...
So the closest multiple of 14 to 239 is 14*17=238
and so 239 = 238+1
1293/14 = 92.357...
So the closest multiple of 14 to 1293 is 14*92=1288
and so 1293 = 1288+5
So
We solve this Diophantine equation:
Since 14 is the coefficient with the smallest
absolute value, 14, we write the 239 and the
1293 in terms of their closest multiple of 14.
239/14 = 17.071...
So the closest multiple of 14 to 239 is 14*17=238
and so 239 = 238+1
1293/14 = 92.357...
So the closest multiple of 14 to 1293 is 14*92=1288
and so 1293 = 1288+5
So
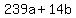  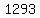 becomes
becomes
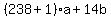  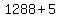
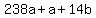  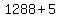 Divide every term through by 14
Divide every term through by 14
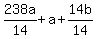  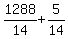
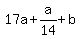  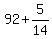 Get all the fractions on the left side,
and other terms on the right side:
Get all the fractions on the left side,
and other terms on the right side:
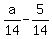  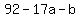 The right side equals to an integer, so the left side
must also equal to that same integer. Let that
integer be N, so:
The right side equals to an integer, so the left side
must also equal to that same integer. Let that
integer be N, so:
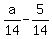   and and 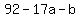  
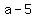  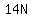
   Substitute in
Substitute in
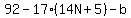  
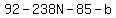  
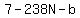  
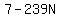   Since b is a digit, the only integer
N can be is 0. So N=0 and
Since b is a digit, the only integer
N can be is 0. So N=0 and
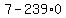  
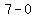  
   Substituting N=0 and b=7 in
Substituting N=0 and b=7 in
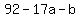  
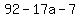  
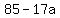  
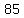  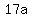
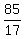  
 So a=5, b=7 and c=3
and the three digit number abc is 573
5 7 3
× 2 4
1 3 7 5 2
Edwin
So a=5, b=7 and c=3
and the three digit number abc is 573
5 7 3
× 2 4
1 3 7 5 2
Edwin
|
|
|