SOLUTION: Using the letters in "PROPOSITIONS" a) How many of the distinguishable arrangements have the two Ps adjacent and the three Os adjacent? b) How many of the distinguishable arr

         PROPOSITIONS
it has 2 P's, 3 O's, 2 S's, 2 I's, 1 R, 1 T, 1 N

That's the distinguishable arrangements of these 9 things
{PP,OOO,R,S,S,I,I,T,N}

The two S's are indistinguishable and the two I's are indistinguishable:

That's 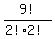 = 90720

First we find the number of distinguishable arrangements:

 = 9979200

Next we find the number that have the 2 P's adjacent.

That is the number of distinguishable arrangements of these 11 things

{PP,O,O,O,S,S,I,I,R,T,N}

The 3 O's, the 2 S's and the 2 I's are indistinguishable:

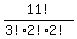That's  = 1663200

So we subtract

9979200 - 1663200 = 8316000

Answer: 8316000

Edwin