There must be at least 3 questions with scores of 3, for if there
were only 2 with scores of 3, that would be only be 6, leaving the
other 15-6 or 9 to be made with 3 scores of 2 or less, which is
impossible.
So the 3 scores of 3 each accounts for 9, so the other 15-9 or 6,
must be made with 3 questions. The only ways to get 6 with
3 questions is 0+3+3, 1+2+3, or 2+2+2.
0+3+3+3+3+3 = 15
1+2+3+3+3+3 = 15
2+2+2+3+3+3 = 15
So there are only 3 basic ways to get 15. However we must permute these
over all 6 questions.
The number of distinct permutations of 0,3,3,3,3,3 is 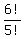

 The number of distinct permutations of 1,2,3,3,3,3 is
The number of distinct permutations of 1,2,3,3,3,3 is 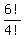

 The number of distinct permutations of 2,2,2,3,3,3 is
The number of distinct permutations of 2,2,2,3,3,3 is 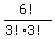

 Answer: 6+30+20 = 56 ways possible to get 15
Edwin
Answer: 6+30+20 = 56 ways possible to get 15
Edwin