Question 838890: How many distinct 4 digit numbers can be formed from 1, 1, 2, 2, 2, 3, 4? I have found many problems with one digit repeating that remove the repeated numbers by division, but I can't figure out what to do with 2 repeating digits aside from lists which are rather inefficient. (7*6*5*4)/(3! +2) is the closest to what I believe to be the answer.
Answer by Edwin McCravy(20066)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1, 1, 2, 2, 2, 3, 4
There are 4 types of 4-digit numbers to get all the permutations of. These 4
types are ABCD, AABC, AABB, and AAAB.
1. ABCD There is only one of this form, 1234. That accounts for 1 form times
4! or 24 ways to arrange it.
2. AABC We can choose the digit for A 2 ways, For each of those ways, we can
choose the B and C any of C(3,2)=3 ways. That accounts for 2×3 = 6 ways to
choose the digits to rearrange, (They are 1123,1124,1134,2213,2214,2234). Each
of these 6 can be rearranged in 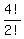 = 12 ways. That's 6×12=72 ways.
3. AABB. This is the number of ways to rearrange 1122 which is = 12 ways. That's 6×12=72 ways.
3. AABB. This is the number of ways to rearrange 1122 which is 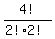 = 6 ways.
4. AAAB. The digit for A must be 2. There are then 3 choices of digits for B.
(These are 2221,2223,2224). Each of those can be arranged = 6 ways.
4. AAAB. The digit for A must be 2. There are then 3 choices of digits for B.
(These are 2221,2223,2224). Each of those can be arranged 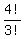 = 4 of each
of this form). That's 12 ways.
Total: 24+72+6+12 = 114 ways.
Edwin = 4 of each
of this form). That's 12 ways.
Total: 24+72+6+12 = 114 ways.
Edwin
|
|
|