Question 836115: if 5 digits number
is formed using odd digits without
repetition,what is the sum of the all
possible number? .
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! There are many ways to get to the answer.
I listed the one that seemed easier for my own mind to understand and calculate.
With some luck, it might sound logical and understandable for you too.
There are 5 odd digits: 1, 3, 5, 7, and 9.
How many 5-digit numbers can we make using those digits without repetition?
We have 5 ways to choose the first digit.
For each of those choices, there will be 4 ways to chose the second digit.
For each set of first and second digit choices, there will be 3 ways to chose the third digit.
For each set of first, second and third digit choices, there will be 2 ways to chose the fourth digit.
all in all, there are  possible 5-digit numbers made from the 5 odd digits without repeating digits.
All 5 of those 5 odd digits are equally likely as the last (units) digit.
The last digit will be a 1 in  of those  numbers.
The last digit will be a 3 in another 24 numbers, a 5 in another 24, a 7 in another 24, and a 9 in another 24 numbers.
All the last digits added up will add up to
 .
The sum of the tens digits will also be  ,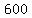
and so will be the sums of the hundreds, thousands, and ten-thousands digits.
The value of the sum of all the numbers will be
|
|
|
