SOLUTION: 1) There exists a 5 digit number N with distinct and non-zero digits such that it equals the sum of all distinct three digit numbers whose digits are all different and are all digi

Algebra ->  Permutations -> SOLUTION: 1) There exists a 5 digit number N with distinct and non-zero digits such that it equals the sum of all distinct three digit numbers whose digits are all different and are all digi      Log On


   

Question 776097: 1) There exists a 5 digit number N with distinct and non-zero digits such that it equals the sum of all distinct three digit numbers whose digits are all different and are all digits of 'N'. Then the sum of the digits of 'N' is a necessarily?
Answer options:
(a) Perfect Square (b) Cube (c) Even (d) None of these
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Suppose the 5-digit number N is  

"ABCDE", that is 

N = 10000A+1000B+100C+10D+E = (9999+1)A+(999+1)B+(99+1)C+(9+1)D+E
= (9999A+999B+99C+9D)+A+B+C+D+E = 9(1111A+111B+11C+D)+A+B+C+D+E

Let S = A+B+C+D+E, then

N = 9K+S where K = 1111A+111B+11C+D
 
There are P(5,3) = 60 3-digit numbers. If we were to add all 
60 of these digits, the 5 digits of N will therefore occur 
12 times among: 

1. the units digits, which will give a sum of 12(A+B+C+D+E)
2. the tens digits, which will give a sum of 120(A+B+C+D+E)
3. the hundreds digits, which will give a sum of digits of 1200(A+B+C+D) 

So the sum of all 60 3-digit numbers will be

12(A+B+C+D+E) + 120(A+B+C+D+E) + 1200(A+B+C+D+E) = 1332(A+B+C+D+E) = 1332S

N = 9K+S = 1332S

So therefore the 5-digit number must be 1332S

N = 9K+S = 1332S
      9K = 1331S
       S = 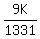9K%2F1331

Since S is an integer, K is a multiple of 1331,

Let K = 1331M

Then S = 9M

and so S is a multiple of 9.

The smallest S could be is 1+2+3+4+5 = 15
The largest S could be is 9+8+7+6+5 = 35

The only multiples of 9 between those values are 18 and 27

If S = 18, M=2, K=1331(2) = 2662, and 

N = 9(2662)+18 = 23976 and 2+3+9+7+6 = 27  

If S = 27, M=3, K=1331(3) = 3993, and 

N = 9(3993)+27 = 35964 and 3+5+9+6+4 = 27 

So there are two possibilities for N, 23976 and 35964,
but in either case the sum of the digits is 27.

27 is 33 so the answer is (b) cube.

Edwin