give a procedure for determining the number of zeros at the end of n!.justify your procedure.
We will use the "floor" function indicated by ⌊x⌋ to denote the largest
integer that does not exceed x. Sometimes this is indicated by int(x).
A factorial is a product of integers. The only thing that will cause a
zero at the end of a product of integers is a factor of 10, which is a
pair of factors 2·5.
n! = 1·2·3·4·5·6···n
There are a lot more factors of 2 contained in the members of the sequence
1,2,3,4,5,6,...,n
than there are multiples of 5 contained in them. So there will always be enough
factors of 2 in n! to pair up with every factor of 5 in n! to cause the pair to
make a factor of 10 causing another zero at the end of 5!
So we only need to count the total number of 5 factors contained in all the members
of the sequence
1,2,3,4,5,6,...,n
Each multiple of 51 contributes a 1st 5 factor.
There are n/⌊ ⌋ of those. Of those,
each multiple of 52 contributes a 2nd 5 factor.
There are n/ ⌊
⌋ of those. Of those,
each multiple of 52 contributes a 2nd 5 factor.
There are n/ ⌊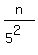 ⌋ of those. Of those,
each multiple of 53 contributes a 3rd 5 factor.
There are n/ ⌊
⌋ of those. Of those,
each multiple of 53 contributes a 3rd 5 factor.
There are n/ ⌊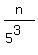 ⌋ of those. Of those,
...
n/ ⌊
⌋ of those. Of those,
...
n/ ⌊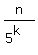 ⌋ will become 0 when 5k
exceeds n.
So the number of 0's at the end of n! is
⌊
⌋ will become 0 when 5k
exceeds n.
So the number of 0's at the end of n! is
⌊ ⌋ + ⌊
⌋ + ⌊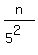 ⌋ + ⌊
⌋ + ⌊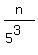 ⌋ + ... + ⌊
⌋ + ... + ⌊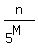 ⌋,
where M is the largest power of 5 that does not exceed n, or even
larger since values of k > M will all be 0.
We can calculate M, which is the largest value of k such that
5k ≦ n
ln(5k) ≦ n
k·ln(5) ≦ n
k ≦
⌋,
where M is the largest power of 5 that does not exceed n, or even
larger since values of k > M will all be 0.
We can calculate M, which is the largest value of k such that
5k ≦ n
ln(5k) ≦ n
k·ln(5) ≦ n
k ≦ 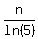 So M = ⌊
So M = ⌊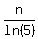 ⌋
You can write the result as a summation:
Number of 0's at end of n! =
⌋
You can write the result as a summation:
Number of 0's at end of n! =  ⌊
⌊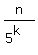 ⌋, where M = ⌊
⌋, where M = ⌊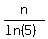 ⌋
Edwin
⌋
Edwin