SOLUTION: I' am preparing for a test and one question that will be similar to the one on the test will be “How many ways can a teacher choose two students from a group of four students?” I l

To explain it to you, I'll have to go into more detail than is
necessary just to solve the problem:

Suppose the students are John, Charles, Susan, and Linda. 

First you work the problem as though it mattered which student 
the teacher spoke first.  That is, we first work the problem as 
though if the teacher says "I choose Susan and John" that would 
be counted as a different situation from the situation in which 
the teacher says "I choose John and Susan".  Then after getting 
that number, we divide that number by 2 to prevent counting those
as 2 separate cases.

There are 4 choices for the student the teacher calls first.  For 
each of those 4 choices of students the teacher calls first, there 
remain 3 choices for the name the teacher calls second.  So that's
4×3 or 12 ways the teacher can fill in the blanks of "I choose ____ 
and _____".  Those are (I'll list them for illustration purposes 
but you don't have to:

1.  "I choose John and Charles".
2.  "I choose John and Susan".
3.  "I choose John and Linda".
4.  "I choose Charles and John".
5.  "I choose Charles and Susan".
6.  "I choose Charles and Linda".
7.  "I choose Susan and John".
8.  "I choose Susan and Charles".
9.  "I choose Susan and Linda".
10.  "I choose Linda and John".
11.  "I choose Linda and Charles".
12.  "I choose Linda and Susan".

But you see in that list that number 1 is the same as number 4,
Number 2 is the same as number 7, etc.,

So therefore we have to divide the number 12 by 2 to keep from
counting those duplicates twice.  That in effect scratches
through all the duplicates:  

1.  "I choose John and Charles".
2.  "I choose John and Susan".
3.  "I choose John and Linda".
4.  "I choose Charles and John".
5.  "I choose Charles and Susan".
6.  "I choose Charles and Linda".
7.  "I choose Susan and John".
8.  "I choose Susan and Charles".
9.  "I choose Susan and Linda".
10.  "I choose Linda and John".
11.  "I choose Linda and Charles".
12.  "I choose Linda and Susan".  

So the answer is 12÷2 or 6

The formula is C(n,r) = 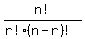 where n=4 is the
number we have to choose FROM, and r=2 is the number we CHOOSE.

C(n,r) =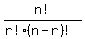 

C(4,2) =  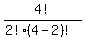=  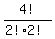=  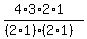= 6

Edwin