SOLUTION: In How Many Ways 50 things Can Be divided In 5 sets,such That 3 sets Contain 12 things each and the remaining 2 sets contain 7 things each?

Algebra ->  Permutations -> SOLUTION: In How Many Ways 50 things Can Be divided In 5 sets,such That 3 sets Contain 12 things each and the remaining 2 sets contain 7 things each?      Log On


   

Question 720627: In How Many Ways 50 things Can Be divided In 5 sets,such That 3 sets Contain 12 things each and the remaining 2 sets contain 7 things each?
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
First let's find the number of ways we can create the sets that contain 12
things each.  Suppose the sets A, B, and C contain 12 things each

We can fill set A in C(50,12) waye, set B in C(38,12) ways and set C(26,12).
That's C(50,12)·C(38,12)·C(26,12) ways.  However we do not want to count
separately any two cases say, Case 1 and Case 2, where in Case 1, set A is 
identical with set C of Case 2, set B is identical with set A of case 2, and
set C is identical with set B of Case 2.  So to eliminate those duplicate
cases we must divide by 3!

So the number of ways to create the 3 sets of 12 is 

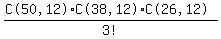%28%22C%2850%2C12%29%22%2A%22C%2838%2C12%29%22%2A%22C%2826%2C12%29%22%29%2F3%21

For each of those ways of creating the sets of 12, we can create the
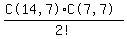2 sets of 7 using the same reasoning  in %28%22C%2814%2C7%29%22%2A%22C%287%2C7%29%22%29%2F2%21 

So the answer is

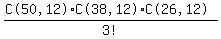
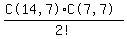%28%22C%2850%2C12%29%22%2A%22C%2838%2C12%29%22%2A%22C%2826%2C12%29%22%29%2F3%21%22%22%2A%22%22%28%22C%2814%2C7%29%22%2A%22C%287%2C7%29%22%29%2F2%21   

or

 

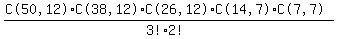or about 9.8×1029

Edwin