Question 715610: I need help with this question. Which are the first four terms in the expansion (2-3y) power of 8?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is a general formula that you were probably given, but probably makes no sense to you.
If your teacher wants it, write it the way it was given to you, but I will tell you what ideas I would use to get the answer (without worrying about formulas).
Since the power is  , there will be , there will be  terms. terms.
I could start with  as a first term, as a first term,
and end with  as a last term, as a last term,
and that is probably what's expected.
All the terms will have combinations of powers of 
and powers of 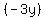 with exponents adding up to with exponents adding up to  . .
The exponents of 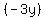 increase from term to term, starting at zero and going up to increase from term to term, starting at zero and going up to  . .
The exponents of  decrease from decrease from  to zero. to zero.
The in-between terms, between the first term and the last term,
will also have combinatorial numbers as extra factors.
(There are many ways to write the symbols for combinatorial numbers,
but I do not know what way you would use in your class,
and I can only write combinatorial numbers in the form 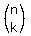 on this website). on this website).
Those combinatorials are all combinations of 
and the other number in the combination is one of the exponents.
Traditionally, it would be the exponent on 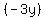 . .
(If you used the exponent of  instead, instead,
the symbol would look different,
but it would calculate as the same number).
So term number  would have would have

with  as the exponent for as the exponent for 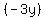 . .
It would also have
 and and
it would also have the combinatorial number

So the fourth term is

The third term has 
 and and 
So the third term is 
The second term has 
 and and 
So the secondd term is 
Then the first four terms would be
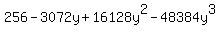
If you have to "show your work", you could just write

A general formula for term number  of the expansion of of the expansion of 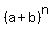
is 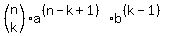
|
|
|