Question 701448: Are there more seven digit numbers with a 1 in them than without a 1 in them? Explain.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A more general question would be:
Are there more n-digit numbers with a 1 in them than without a 1 in them?
The fraction of n-digit numbers without a 1 in them
(the probability that 1 would not be any of the n digits) is

because the first digit cannot be zero,
and it would not be 1 for  of the possible digits, of the possible digits,
while the other 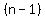 digits have no restriction, digits have no restriction,
and would not be 1 in 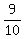 of the cases. of the cases.
If you were taught the name you would recognize that as a
"geometric sequence" or "geometric progression".
Even if you did not know of a name for them,
it is clear that the fraction of n-digit numbers without a 1 in them
(or the probability of an n-digit number not having a 1)
decreases as towards zero as  increases. increases.
It is  for 1-digit numbers, for 1-digit numbers,
 for 2-digit numbers, for 2-digit numbers,
and keeps getting smaller as we keep including more 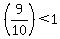 factors. factors.
For 7-digit numbers the fraction of them without a 1 is
 , ,
so there are  7-digit numbers with a 1 in them than without a 1 in them. 7-digit numbers with a 1 in them than without a 1 in them.
EXTRAS:
Calculating 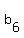 , I would find that , I would find that 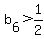 , ,
but how would I find the value of  where where 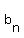 becomes smaller than becomes smaller than  without calculating and tabulating without calculating and tabulating 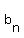 values for n=1, 2, 3, ...? values for n=1, 2, 3, ...?
That's where you use logarithms.
Sorry, I'm getting carried away.
|
|
|