Question 638033: Mr. and Mrs. Richardson want to name their new daughter so that her initials (first, middle, and last) will be in alphabetical order with no repeated initial. How many such triples of initials can occur under these circumstances?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let's assume that are only 5 letters in the alphabet.
let's assume those letters are nopqr
let's assume the last name initials have to be r.
we could then have:
for the q in front of the r, we could have:
pqr
oqr
nqr
for the p in front of the r, we would have:
opr
npr
for the o in front of the r, we could have:
nor
total number of possibilities looks like 3 + 2 + 1
we started with 5 letters.
our descending numbers started with 5 - 2 = 3 letters that could be substituted for each other while retaining the order.
the letter r is the 18th letter in the alphabet.
subtract 2 from that and you get 16 letters that could be interchanged the first time around, then 15, then 14, then 13, ..... down to 1.
this looks like an arithmetic sequence where the common difference is 1.
out starting number is 1 and our ending number is 16.
the formula for the last number in an arithmetic progression is L = a + (n-1)d
if d is equal to 1 and a is equal to 1, and n is equal to 16, then the last number in this sequence wuld be 1 + 15*1 = 16.
the sum of the numbers in this sequence is given by the formula S = n * (a + L) / 2
this would be equal to 16 * (1 + 16) / 2 which is equal to (16*17)/2 which is equal to 8*17 which is equal to 136.
that's what i think.
i could be way off base but, assuming i understood the problem correctly, i believe this is a good answer.
i'll do the small one again just to make sure the logic is correct.
assume the letters abcdefg and the last name starts with a g.
then you would have:
efg
dfg
cfg
bfg
afg
followed by:
deg
ceg
beg
aeg
followed by:
cdg
bdg
adg
followed by:
bcg
acg
followed by
abg
that's 5 + 4 + 3 + 2 + 1 = 15 possible combinations.
number of letters to start with was 7
starting number was 7-2 = 5
it looks like it's a good solution.
check it out and see if it agrees what you think.
Answer by ikleyn(53411)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Mr. and Mrs. Richardson want to name their new daughter so that her initials (first, middle, and last) will be in
alphabetical order with no repeated initial. How many such triples of initials can occur under these circumstances?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This is a good problem. I will help you to solve it.
The last name of the newborn child should be Richardson, so the last letter of the triple must be R.
English alphabet has 26 letters, and 'R' is the 18-th letter in the English alphabet.
So, all possible triples are of the form ABR, where A and B are two different letters
of the English alphabet preceding 18-th letter 'R'.
For this pair (AB) in the alphabetical order, there are 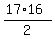 = 8*17 = 136 possible different opportunities.
Hence, 136 triples of initials can be formed, as parents Mr. and Mrs. Richardson wish. <<<---=== ANSWER = 8*17 = 136 possible different opportunities.
Hence, 136 triples of initials can be formed, as parents Mr. and Mrs. Richardson wish. <<<---=== ANSWER
Solved.
|
|
|