6 boys and 5 girls are to be seated around a table. Find the number of ways that this can be done in each of the following cases.
a. there are no restrictions
First we find the number of ways they could line up in a single file to march
to the table and then divide by the number of ways the table could be rotated.
They could line up in a single file in 11! ways and the table could be rotated
11 ways. So the answer is
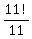= 10! = 3628800
b. no 2 girls are adjacent
Let's seat the 5 girls first. The girls can be lined up in 5! ways and the
table can be rotated 5 ways, so we can seat the girls in 5!/5 = 4! = 24 ways.
There are 5 spaces between the girls. We pick 5 of the boys to go in those 5
spaces in 6C5 = 6 ways, and we can arrange those 5 boys in 5! = 120 ways. We
have one boy left over to seat, so he will have to sit next to a boy. He can
pick the boy to sit next to in 5 ways, and he can pick whether to sit on his
left or his right in 2 ways, so that's
24·6·120·5·2 = 172800.
c. all girls form a single block
So the boys must also form a single block.
Then the single block of girls can be arranged in 5! ways. The single block of
boys can be arranged in 6!.
Answer 5!6! = 120·720 = 86400
d. a particular girl G is adjacent to two particular B1 and B2
That trio can be seated 2 ways, B1,G,B2 or B2,G, B1. The remaining 8 people
can sit anywhere.
So with B1,G,B2, we have to seat 9 "things" around the table, 8 singles and 1
trio. We could arrange them in a line in 9! ways, then the table could be
rotated in 9 ways, so that 9!/9 = 8! = 40320 ways. That's for the trio sitting
B1,G,B2. But they could also sit B2,G,B1, so that's another 40320.
Answer 8!·2 = 40320·2 = 80640 ways.
Edwin
