The number of ways in which 12 students can be equally divided into three groups is.
First we will work the problem assuming there that there is
a GOOD group, a BETTER group and a BEST group.
We can choos 4 students for the GOOD group in 12C4 or 495
For each of those 495 ways to choose 4 for the GOOD group, there
are 8C4 or 70 ways to choose the BETTER group.
That's 12C4·8C4 or 34650 ways to choose the GOOD and BETTER groups.
For each of those 34650 ways to choose the GOOD and BETTER groups, there
are 4C4 or 1 way to choose the BETTER group.
So there are 12C4·8C4·4C4 = 34650 ways to choose the GOOD, BETTER, and
BEST groups.
-----------------
However we now remember that there were really no GOOD. BETTER, and BEST
groups at all. Suppose the 12 people were {A,B,C,D,E,F,G,H,I,J,K,L}
Suppose we look at a sample situation:
The 34650 counts all 3! or 6 of these:
GOOD group = {B,H,J,L}
BETTER GROUP = {D,F,G,I}
BEST group = {A,C,E,K}
GOOD group = {B,H,J,L}
BETTER GROUP = {A,C,E,K}
BEST group = {D,F,G,I}
GOOD group = {D,F,G,I}
BETTER GROUP = {B,H,J,L}
BEST group = {A,C,E,K}
GOOD group = {D,F,G,I}
BETTER GROUP = {A,C,E,K}
BEST group = {B,H,J,L}
GOOD group = {A,C,E,K}
BETTER GROUP = {D,F,G,H}
BEST group = {B,H,J,L}
GOOD group = {A,C,E,K}
BETTER GROUP = {B,H,J,L}
BEST group = {D,F,G,H}
separately. But we do not consider these as separate groupings.
And the 34650 similarly counts every arrangement 3! or 6 times
too many. Therefore we most divide the 34650 by 6. The answer is
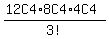 =
= 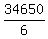 = 5775
Edwin
= 5775
Edwin