SOLUTION: total number of ways in which six 't' and four '-' signs can be arranged in a line such that no two '-' signs occur together is ?

Let's examine a random arrangement of 6 "t"s and 4 "-"s:

Suppose we look at this arbitrary arrangement:

-  -  t  t  -  t  t  t  -  t

Let's number the positions:

1  2  3  4  5  6  7  8  9 10
-  -  t  t  -  t  t  t  -  t

Notice that there are 10 positions. This particular one 
chooses positions 1,2,5, and 9 for the "-"s and the
rest has "t"'s 

So there are 10 positions, and we choose 4 of them

to put the -'s.  That's "10 choose 4" or 10C4 or C(10,4) or

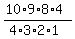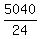 =  = 210 ways

Edwin