If we could tell the two d's apart, and the three e's apart, and the
word were written like this:
decrEᕮD
then the answer would be 7! = 5040
However if we take a random permutation of that, say
cᕮDerdE
There are 3! ways to arrange the ᕮ, e, and E within that permutation,
and every other permutation of decrEᕮD is the same way, so that
means that the 7! or 5040 counts the same permutation 3! of 6 times too
many, so we must divide by 3! or 6.
But there are also 2! ways the D and d can be arranged, so we must
also divide by 2!, since we cannot tell the D from the d when they are
both small d's. Therefore the number of distinguishable ways when
all the e's look alike and both the d's look alike, is given by
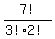 =
= 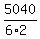 =
= 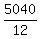 = 420
Edwin
= 420
Edwin