Question 500395: find the number of ways to arrange the letters in MINIMUMS
Found 2 solutions by Jstrasner, kevwill:
Answer by Jstrasner(112)   (Show Source):
You can put this solution on YOUR website! Hey,
So for this problem we need to figure out how many combinations of letters there can be.
There are 8 possible letters in the first letter spot, 7 for the second letter spot, 6 for the 3 letter spot, 5 for the 4 letter spot, 4 for the 5 letter spot, 3 for the 6 letter spot, 2 for the 7 letter spot and lastly 1 for the 8 letter spot:
__ x __ x __ x __ x __ x __ x __ x __ => 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40,320 possible way to arrange the letters in MINIMUMS.
I hope this helps!
Answer by kevwill(135)  (Show Source):
You can put this solution on YOUR website! I think the original solver overlooked the fact that there are duplicated letters in the word that reduce the number of distinct permutations. There are 2 I's and 3 M's, so the actual number of different ways to arrange the letters in MINIMUMS is 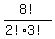 = (8*7*6*5*4*3*2*1)/((2*1)*(3*2*1)) = 3360}}}
|
|
|
