Question 500253: You have the word FEEBLENESS, in a random arrangement, what is the probabilty that exactly three E's will be together?
Found 2 solutions by Edwin McCravy, stevegalloway:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
FEEBLENESS
To have three E's together we have to find the number of all cases of
distinguishable arrangements of these 8 things
B,E,F,L,N,S,S,(EEE)
and divide it by the number of all cases of distinguishable
arrangements of these 10 things:
B,E,E,E,E,F,L,N,S,S,
The answer is 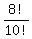 = = 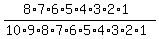 = = 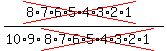 = = 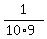 = =  However you may think it's not that because there are indistinguishable letters E and S. But we must divide
both numerator and deminator by the same number to "unorder" them.
To explain that:
Let's start out making the E's and S's distinguishable
B, E1, E2, E3, E4, F, L, N, S1, S2
There would be 10! ways to arrange those if we could tell the difference between the E's and the S's.
But we can't. So 10! counts this too many times. We need to find out how many times too many 10!
counts any arrangement.
To find that, look at an arbitrary arranglement of those 10 distinguishable things, say this one:
LE4FS2BE2NS1E3E1
There are 4! ways the 4 subscripts of E could be arranged, and for each of those ways, there are 2!
ways the subscripts of S could be arranged. So the number of times too many which 10! counts the
arrangement of LEFSBENSEE is 4!2!
However, any arbitrary distinguishable arrangement of the 8! when the E's
are together, say,
S2L(E4E1E3)FBE2S1L
is also counted 4!2! times too many among the 8!, so we would divide it by the same number to
"unorder" it. So technically we would do it this way:
However you may think it's not that because there are indistinguishable letters E and S. But we must divide
both numerator and deminator by the same number to "unorder" them.
To explain that:
Let's start out making the E's and S's distinguishable
B, E1, E2, E3, E4, F, L, N, S1, S2
There would be 10! ways to arrange those if we could tell the difference between the E's and the S's.
But we can't. So 10! counts this too many times. We need to find out how many times too many 10!
counts any arrangement.
To find that, look at an arbitrary arranglement of those 10 distinguishable things, say this one:
LE4FS2BE2NS1E3E1
There are 4! ways the 4 subscripts of E could be arranged, and for each of those ways, there are 2!
ways the subscripts of S could be arranged. So the number of times too many which 10! counts the
arrangement of LEFSBENSEE is 4!2!
However, any arbitrary distinguishable arrangement of the 8! when the E's
are together, say,
S2L(E4E1E3)FBE2S1L
is also counted 4!2! times too many among the 8!, so we would divide it by the same number to
"unorder" it. So technically we would do it this way:
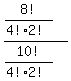  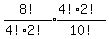  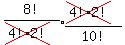  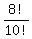  Edwin
Edwin
Answer by stevegalloway(1)   (Show Source): (Show Source):
You can put this solution on YOUR website!
QUESTION: You have the word FEEBLENESS, in a random arrangement, what is the probability that exactly three E's will be together?
SOLUTION: Our solution will not be feeble!
We first find the number of ways to arrange the E's without restrictions. We have 10 positions in which to place the four E's. Since the E's are identical, we do not care about their order. Hence, there are   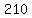 ways to position the four E's. ways to position the four E's.
Second, we find the number of ways to arrange the E's with exactly three E's together. Below are the 8 positions for the group of three E's. The dashes represent positions where the fourth E could be located, and the x's represent positions where the fourth E cannot be located.
1) EEEx------ leaves 6 possible positions for the fourth E
2) xEEEx----- leaves 5 possible positions for the fourth E
3) -xEEEx---- leaves 5 possible positions for the fourth E
4) --xEEEx--- leaves 5 possible positions for the fourth E
5) ---xEEEx-- leaves 5 possible positions for the fourth E
6) ----xEEEx- leaves 5 possible positions for the fourth E
7) -----xEEEx leaves 5 possible positions for the fourth E
8) ------xEEE leaves 6 possible positions for the fourth E
To meet the requirement, we must have situation 1, 2, 3, 4, 5, 6, 7, or 8 above, for which each EEE location is unique. Hence, we add the possibilities. Therefore, we have 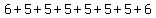   ways to arrange the E's with exactly three together. ways to arrange the E's with exactly three together.
Finally, to find the probability of having exactly three E's together, we divide the ways to arrange the E's with exactly 3 together by the ways to arrange the E's in general. We have   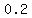    . .
Note that, since the other 6 letters are not E's, their order is ultimately irrelevant. If we include the different ways to arrange these additional letters in the 6 remaining positions, the corresponding factors cancel out of the final probability fraction. (Please try this for practice!)
(Note that this solution was tested by computer simulation.)
|
|
|