Question 452441: There are a number of people in a roo and each person shakes hands once with each of the other people.
a) If there are 5 people in the room, how many handshakes have taken place?
b) If there are 6 people in the room, how many handshakes have taken place?
c) If there are 7 people in the room, how many handshakes have taken place?
d) If there are n people in the room, how many handshakes have taken place? Write a recursive formula and explicit formula.
e) Where are these numbers on Pascal's Triangle?
f) If there were 190 handshakes altogether, how many people were in the room?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
So let's ay the room has only A and B---two people.
there is one handshake
(A with B).
Three people (A, B, and C), there are three handshakes
(A with B and C; B with C).
Now, let's try four people (A, B, C, and D), there are six handshakes
(A with B, C, and D; B with C and D; C with D).
So if we have n-1 people, the number of handshakes is the sum of the first n numbers. This is n(n-1)/2
a) If there are 5 people in the room, how many handshakes have taken place?

b) If there are 6 people in the room, how many handshakes have taken place?

c) If there are 7 people in the room, how many handshakes have taken place?

d) If there are n people in the room, how many handshakes have taken place?
Write a recursive formula and explicit formula.
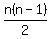
e) Where are these numbers on Pascal's Triangle?
these are triangular numbers
f) If there were 190 handshakes altogether, how many people were in the room?

Another way to think of this, if you have done some combinations, is for  people, in how many ways can you pick two. This is people, in how many ways can you pick two. This is 
for 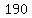 people people
|
|
|