SOLUTION: 12 people are to be grouped into 3 clubs, 4 people in each club. Each club is then electing a president and a vice president. In how many ways can this be done?

First we will work the problem as though the clubs were ordered. That is, we
will consider this case:

Club 1 consists of Mary as President, John as Vice-President, and non-officer
members Sam and Sue.
Club 2 consists of Henry as President, Carol as Vice-President, and non-officer
members Elain and Luke.
Club 3 consists of Katy as President, Jimmy as Vice-President, and non-officer
members Mark and Sally.

to be counted as a separate case from this

Club 1 consists of Henry as President, Carol as Vice-President, and non-officer
members Elaine and Luke.
Club 2 consists of Katy as President, Jimmy as Vice-President, and non-officer
members Mark and Sally.
Club 3 consists of Mary as President, John as Vice-President, and non-officer
members Sam and Sue.

You see that the two cases above are really the same case.  There are 3! or 6
ways we could rearrange this same case, so when we finish we will divide by 3!
to "unorder" the clubs in the final count.

But assuming the clubs are ordered 1,2, and 3 we have this:

Club 1:   { President, Vice-President, club member, club member }
Club 2:   { President, Vice-President, club member, club member }
Club 3:   { President, Vice-President, club member, club member }

We can 

1. choose Club 1's President any of 12 ways.  For each of those
ways we can

2. choose Club 1's Vice-President any of 11 ways.  For each of 
those ways we can 

3. choose Club 2's President any of 10 ways.  For each of those
ways we can

4. choose Club 2's Vice-President any of 9 ways.  For each of those
ways we can

5. choose Club 3's President any of 8 ways.  For each of those
ways we can

6. choose Club 3's Vice-President any of 7 ways.  For each of those
ways we can

7. choose Club 1's other two non-officer members any of 6C2 ways  For
each of those ways we can

8. choose Club 2's other two non-officer members any of 4C2 ways  For each of
those ways we can

9. choose Club 3's other two non-officer members any of 2C2 ways. (That's just
1 way!)

So considering the clubs to be ordered, the count would be

12*11*10*9*8*7*(6C2)*(4C2)*(2C2)

Then as we said in the beginning we must divide that by 3! to "unorder"
the 3 clubs:



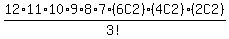The final count comes out to 

9979200

Edwin