SOLUTION: Number of ways in which p positive and n negative signs may be placed in a row so that no two negative signs shall be together ?. More than an answer I need the reasoning behind

Number of ways in which p positive and n negative signs may be placed in a row
so that no two negative signs shall be together ?.  More than an answer, I need
the reasoning behind the answer. 

Suppose you have p=10 positive signs and n=4 negative signs:

   +   +   +   +   +   +   +   +   +   +
 1   2   3   4   5   6   7   8   9  10   11

Since negative signs cannot come together, we can only put one negative
sign before any of the 10 positive signs, plus we can also place a negative
sign after the 10th positive sign.  So there are 11 places we can insert a
negative sign, and we must choose 4 of those to place the 4 negative signs:

So the answer for this specific case is 11C4

The reasoning is the same for any number p of positive signs and any number
n of negative signs.  We can only put one negative sign before any of the p
positive signs, plus we can also place a negative sign after the pth positive
sign.  So there are p+1 places we can insert a negative sign, and we must
choose n of those to place the n negative signs:

So the answer is "(p+1) choose n" which is also called "the number of
combinations of p+1 things taken n at a time".

It is sometimes written 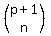, sometimes written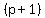  and sometimes written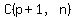 

It is calculated as 

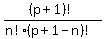You need not worry if you have too many negative signs, i.e., if n > p+1,
for the number of combinations is always defined as 0 in those cases.

Edwin