SOLUTION: A permutation is selected at random from the letters SEQUOIA. what is the probability that it has Q in the fourth position and ends with a vowel?

To have a SUCCESSFUL arrangement of the letters:

_ _ _ Q _ _ vowel

 
There is 1 way to place the Q in 4th place.
There are 5 ways to place a vowel on the right end, E, U, O, I or A.
There are 5 ways to place a letter in the first place (what hasn't been placed already).
There are 4 ways to place a letter in the second place (what hasn't been placed already).
There are 3 ways to place a letter in the third place (what hasn't been placed already).
There are 2 ways to place a letter in the fifth place (what hasn't been placed already).
There is 1 way to place a letter in the sixth place (what hasn't been placed already).

That's 1x5x5x4x3x2x1 = 600 ways to make a SUCCESSFUL arrangement of the letters.

To have ANY arrangement of the 7 letters, successful or not:

_ _ _ _ _ _ _

There are 7 ways to place a letter in the 1st place, S, E, Q, U, O, I, or A. 
There are 6 ways to place a letter in the 2nd place (what hasn't been placed already).
There are 5 ways to place a letter in the 3rd place (what hasn't been placed already).
There are 4 ways to place a letter in the 4th place (what hasn't been placed already).
There are 3 ways to place a letter in the 5th place (what hasn't been placed already).
There are 2 ways to place a letter in the 6th place (what hasn't been placed already).
There is 1 way to place a letter in the 7th place (what hasn't been placed already).

That's 7x6x5x4x3x2x1 = 7! = 5040 ways to make ANY arrangement of the letters, successful or not.

-------------------------------------

The desired probability is then the fraction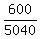 
which reduces to  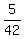by dividing top and bottom by 120.

Edwin