Question 249859: For the expansion of (k+t)^22 ,state
a. the number of terms
b. the degree of each term
c. the first 4 terms in the expansion, without coefficients
d. the coefficients of the first three terms
My answers
a. 23
b. 22
c. k^22, k^21t, k^20t^2, and k^19t^3
d. 1, 22 , not sure what the 3rd term is???
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The binomial expansion is easier if you don't call the first
term "the first term" but instead call it "the zero-th term",
and call the second term "the first term" and then call the last
term the nth term, (which is really the (n+1)st term).
If you use that "start counting from 0 instead of 1" convention
then the Rth term of 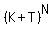 is
is 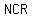 which is sometimes written which is sometimes written 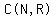 and sometimes
written and sometimes
written  but it always means but it always means 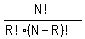 ,
the 0th term's coefficient is ,
the 0th term's coefficient is 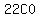 or or 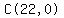 or or 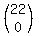 which means
which means  The 1st term's coefficient is
The 1st term's coefficient is 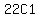 or or 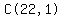 or or 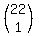 which means
which means  =
=  =
= =
=  = =
 The 2nd term's coefficient is
The 2nd term's coefficient is  or or 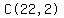 or or 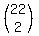 which means
which means  =
=  =
= =
=  = =
 You can also just skip all that cancelling and observe
the pattern of what's always left after cancelling:
If you needed the 3rd term's coefficient (really the 4th term's),
it would be
You can also just skip all that cancelling and observe
the pattern of what's always left after cancelling:
If you needed the 3rd term's coefficient (really the 4th term's),
it would be
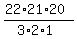 If you needed the 4th term's coefficient (really the 5th term), it would be
If you needed the 4th term's coefficient (really the 5th term), it would be
 If you needed the 5th term's coefficient (really the 6th term), it would be
If you needed the 5th term's coefficient (really the 6th term), it would be
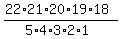 etc., etc.
So to get the numerator of any term's coefficient, you start with
the outer exponent, and multiply it by 1 less, then 1 less, etc.
until you have as many factors as the number of term (starting
counting from zero, not 1). Then the denominator is just that
number factorial. There are always as many factors on top
as the number of term (starting counting form 0, not 1). And
of course the denominator has that same number of factors, too.
Edwin
etc., etc.
So to get the numerator of any term's coefficient, you start with
the outer exponent, and multiply it by 1 less, then 1 less, etc.
until you have as many factors as the number of term (starting
counting from zero, not 1). Then the denominator is just that
number factorial. There are always as many factors on top
as the number of term (starting counting form 0, not 1). And
of course the denominator has that same number of factors, too.
Edwin
|
|
|