Question 207453: There are 16 books on a book shelf.In how many ways can 6 of these be selected,if a selection must not include two neighbouring books?
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are 16 books on a book shelf.In how many ways can 6 of these be selected,if a selection must not include two neighbouring books?
Suppose the 16 books are labeled A through P
A B C D E F G H I J K L M N O P
To make the problem a bit easier, we put an extra 17th book,
Q, on the far right end of the shelf which we agree NEVER
to choose. That way, every book we DO choose will have a
right neighbor that we DO NOT choose.
With the extra book on the right end, the 17 books are now
A B C D E F G H I J K L M N O P Q
Now let's look at an arbitrary sample selection, say, we
choose these books: C, F, H, K, M, and P.
Now let's put an X under each of those that we chose:
A B C D E F G H I J K L M N O P Q
X X X X X X
After each book on the shelf which we select,
there is always a book just to the right of it that
we DO NOT select.
Let's pair each of the 6 chosen books with its neighbor
on the right which we did not choose:
A B (C D) E (F G)(H I) J (K L)(M N) O (P Q)
Now under each pair of books, we write a 1 and under each
single non-paired book we write a 0:
A B (C D) E (F G)(H I) J (K L)(M N) O (P Q)
0 0 1 0 1 1 0 1 1 0 1
So now we see that this sample selection of books
amounts to the string
00101101101
all 1's and 0's. There are 6 1's and the rest 0's.
So we have 11 places in the string, and we must choose
6 of those 11 places for the 1's to go, and the rest
will be 0's. Regardless of which choice we make there
will always be 6 1's. So we have 11 places in the
string and we must choose 6 of them for the 1's to go.
So that is
"11 things, choose 6"
Sometimes that is called
"The number of combinations of ll things taken 6 at a time"
That can be written in any one of the following ways:
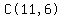 , ,  , , 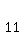  , , 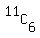 , or , or 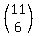 And the formula is
And the formula is
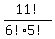 = =  Edwin
Edwin
|
|
|