Question 175399: Please help me solve the problem: A teacher has a set of 12 problems to use on a math exam. The teacher makes different versions of the exam by putting 10 questions on each exam. How many different exams can the teacher make?
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! before i start, i'll explain n! if you don't already know.
n! = n * (n-1) * (n-2) * ..... * (n-n+1).
an example:
5! = 5*4*3*2*1
---
you want a combination of 10 exams out of a possible 12.
the formula for combinations is:
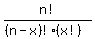
where n is the total number of possibilities,
and x is the total number in each set.
---
in your problem, n = 12, and x = 10.
this would be 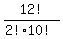
this is the same as:
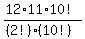
the 10! cancels out.
2! = 2*1 = 2
this leaves:
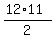
this becomes 6 * 11 = 66
---
teacher should be able to make 66 exams with 10 problems each out of the total of 12 problems.
---
lots of the problems will be duplicated but each exam will have at least 1 problem that is different.
---
i could show you how this works with a smaller number.
---
take a total of 5 problems with exams that are 3 problems each.
this becomes 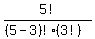
which becomes:
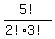
which becomes:

which becomes:

which equals 10 exams with 3 out of the 5 problems each as follows:
problems in each exam:
1,2,3
1,2,4
1,2,5
1,3,4
1,3,5
1,4,5
2,3,4
2,3,5
2,4,5
3,4,5
each set is different from the other set in its entirety even though the same problem can appear in different sets.
---
order doesn't count, so
[1,2,3] is considered the same set as [3,2,1] since they both contain the same elements regardless of the order in which they appear.
---
i could do the same with the exams of 10 problems each out of 12 problems but it would take longer to show you.
---
a beginning of how i would do it is as follows:
problems in each exam of 10 out of 12:
1,2,3,4,5,6,7,8,9,10
1,2,3,4,5,6,7,8,9,11
1,2,3,4,5,6,7,8,9,12
1,2,3,4,5,6,7,8,10,11
1,2,3,4,5,6,7,8,10,12
1,2,3,4,5,6,7,8,11,12
1,2,3,4,5,6,7,9,10,11
1,2,3,4,5,6,7,9,10,12
1,2,3,4,5,6,7,9,11,12
1,2,3,4,5,6,8,9,10,11
1,2,3,4,5,6,8,9,10,12
1,2,3,4,5,6,8,9,11,12
1,2,3,4,5,6,8,10,11,12
1,2,3,4,5,6,9,10,11,12
1,2,3,4,5,7,8,9,10,11
1,2,3,4,5,7,8,9,10,12
etc.......
---
it's a pain in the neck to do, but if you went through all the possible combinations you would see that there are 66 of them if each set has 10 problems out of the total universe of 12.
---
|
|
|