Question 175393: How many different permutations can you make with the letters in the word seventeen?
Found 2 solutions by gonzo, Edwin McCravy:
Answer by gonzo(654)   (Show Source):
You can put this solution on YOUR website! the general formula for a permutation of a set of x units out of a possible set of n units is given by the equation:
---
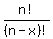
you have 9 possible letters, so n would = 9 in this case.
you will be extracting a set of 9 letters from this, so x would also be 9 in this case.
---
the number of possible ways this set of 9 letters can be arranged if order is important (permutation is an ordered set) are then given by the equation:
9! / (9-9)!
which becomes:
9! / 0!
which becomes:
9!
because 0! = 1
---
the resultant answer would be 362880
---
this answer assumes that the same letter can be used more than once.
---
the word seventeen has 4 e's and 2 n's
to distinguish between them you would have to label them differently.
something like:
e1, e2, e3, e4, e5
n1, n2
---
you can also assign numbers to each letter so that they show up as unique.
something like:
s = 1, first e = 2, v = 3, second e = 4, etc.
---
if multiple occurrences of the same letter are not allowed, then the problem becomes different.
---
the assumption here would be that multiple occurrences of the same letter count as one occurrence.
---
in that case, you have 5 unique letters to choose from.
those are:
s, e, v, n, t
---
the number of permutations you could make with these letters would be 5! which equals 120
---
to help you see this, take a word with smaller number of letters in it.
---
let the word "see" be the problem.
---
assuming the ssme letter can be used more than once, the number of permutations would be 3! = 6
let s = 1, first e = 2, second e = 3
this will make it easier to show:
the individual permutations are:
123
132
213
231
312
321
---
assume that multiple occurrences of the same letter count as one occurrence of that letter.
then the possible letters that can be used are s and e only.
this would be 2!
let s = 1, e = 2
permutations are:
12
21
---
the answer to your question is therefore:
---
if multiple occurrences of the same letter count as a separate occurrence of tht letter, then the number of permutations is 9! = 362880
---
if multiple occurrences of the same letter count as 1 occurrence of that letter, then the number of permutations is 5! = 120
---
Answer by Edwin McCravy(20055)  (Show Source):
You can put this solution on YOUR website!
Warning: Gonzo's solution is incorrect!
Edwin's solution:
How many different permutations can you make with the letters in the word seventeen
There are two methods for finding this:
Method 1:
and
Method 2:
Explanation of method 1:
Since "seventeen" is a 9-letter word, there are 9 positions
to place the letters.
We can choose any 1 of the 9 positions for the "s".
That's 9C1 ways to place the s. After placing it, that
leaves 8 positions to fill.
We can then choose any 4 of the 8 remaining positions
for the 4 "e"'s. That's 8C4 ways to place the 4 e's. After
placing them, that leaves 4 positions to fill.
We can then choose any 1 of the 4 remaining positions
for the "v". That's 4C1 ways to place the "v". After
placing it, that leaves 3 positions to fill.
We can then choose any 2 of the 3 remaining positions
for the 2 "n"'s. That's 3C2 ways to place the 2 "n"'s. After
placing them, that leaves only 1 position to fill.
So we can chose the position for the "t" in only 1C1 or 1 way.
So the answer using method 1, is
Explanation of Method 2:
First pretend that the 4 e's are all different colors, so that we
could tell them apart. And also pretend that the 2 n's are different
colors, so that we can tell them apart too.
That is let's pretend that the word "seventeen" is spelled with
colored letters, like this
seventeen
So there would be 9! or 362880 ways to arrange them if we could
tell the e's apart and also tell the n's apart.
So one random sample of such an arrangment of "seventeen" is,
say, this:
nevtesene
Now within this one particular sample arrangement there are 4! ways
we can arrange the colors of the e's and there are 2! ways we can
arrange the colors of the n's.
So that's 4!2! or 48 ways to move the e's and n's around in that
one particular sample. And every one of these would be a
case of the arrangement "nevtesene".
Every sample would be the same, so that means that the 9! or 362880
counts every arrangement 4!2! or 48 times too many, so we must
divide it by 48 to get the correct answer. So the answer, using
method 2 is
Edwin
|
|
|
