Question 175180: Please help me on these questions, I've tried for hours and i'm torn. I beg you.
Solve each equation.
1. 2x3 – 5x2 – 3x + 2 = 2
2. x3 + 64 = 0
A. -4,2 +/- 2i/3
B. 3,-1 +/- 2i/3
C. -4,2 +/- 3i/4
D. 4,2 +/- 2i/3
3. x4 – 8x2 – 9 = 0
A. 2,-3,4i,i
B. -3,3,i,-i
C. 2,-3,4i,-i
D. 3,i,-i
Use the Rational Root Theorem to find all the roots of each equation.
4. x3 + 9x2 + 19x – 4 = 0
5. 2x3 – x2 + 10x – 5 = 0
6. Two roots of a polynomial equation with real coefficients are 2 + 3i and . Find two additional roots. Then find the degree of the polynomial.
A. 2-4i,-/8; Degree2
B. 2-3i,/7; Degree4
C. 2-3i,-/7;Degree4
D. 2+4i,-/9;Degree12
Evaluate each expression.
7. 6P4
8. 5(3P2)
9. 5C2 + 5C1
10. 7C3/7C4
11. There are 14 different types of boxed nails in the hardware store. You plan to buy 5 different types of boxed nails. How many different combinations are there?
12. In how many different orders can six colored blocks be chosen from a set of 23 different blocks?
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. 
Add -2 to both sides:

Factor out an x

Apply the Zero Product Rule:
 or or  . Just solve the quadratic (it factors if you want to take the time, or just use the quadratic formula) . Just solve the quadratic (it factors if you want to take the time, or just use the quadratic formula)
2. 
 . We know that . We know that  is the cube root of is the cube root of 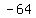 , therefore , therefore  must be a factor of must be a factor of  . .
Use polynomial long division or synthetic division to divide  into into  . Remember to expand the dividend to include the missing 2nd and 1st degree terms. ( . Remember to expand the dividend to include the missing 2nd and 1st degree terms. (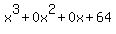 ) You will, of course, get a quadratic polynomial as a quotient and a zero remainder. Set the quadratic equal to zero and solve for the two roots. This one won't factor so you will have to either complete the square or use the quadratic formula. ) You will, of course, get a quadratic polynomial as a quotient and a zero remainder. Set the quadratic equal to zero and solve for the two roots. This one won't factor so you will have to either complete the square or use the quadratic formula.
If you need help with polynomial long division or synthetic division, Wikipedia has an excellent article (http://en.wikipedia.org/wiki/Polynomial_long_division)
3. 
Let  , then , then 
Now solve the quadratic  . .  and and  , so , so 
Hence:  or or  , but , but  so so  or or  so so  or or  or or  or or 
4. The Rational Root Theorem says that if a polynomial equation has rational roots, they must be of the form 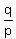 or or  where where 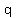 is a factor of the constant term and is a factor of the constant term and  is a factor of the high order term coefficient. For is a factor of the high order term coefficient. For  , the coefficient on the high order term is 1, and the possible factors of the constant term are 1, -1, 2, -2, 4, and -4. Therefore the only possible rational roots are 1, -1, 2, -2, 4, and -4. That means that if the equation has rational roots at all, , the coefficient on the high order term is 1, and the possible factors of the constant term are 1, -1, 2, -2, 4, and -4. Therefore the only possible rational roots are 1, -1, 2, -2, 4, and -4. That means that if the equation has rational roots at all,  , ,  , , 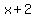 , ,  , ,  , and/or , and/or  must be a factor of the polynomial. must be a factor of the polynomial.
If the result of dividing the original polynomial by any of the listed possible binomial factors results in a quotient with no remainder, then that binomial is, in fact, a factor. The quotient in this case will be a quadratic that can be solved by ordinary means to obtain the remaining roots.
5. Works the same as number 4, except that your possible roots are 1, -1, 5, -5, 1/2, -1/2, 5/2, -5/2.
6. Can't do this one completely because you only listed one of the two given roots. I can tell you that one of the missing roots is 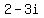 because complex roots ALWAYS come in conjugate pairs because complex roots ALWAYS come in conjugate pairs 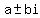 . Irrational roots also always come in conjugate pairs: . Irrational roots also always come in conjugate pairs:  . .
7, 8, 9, 10: The formula for Permutations is: P(n,r) =  . So problem 7 would be P(6,4) = . So problem 7 would be P(6,4) =  . .
The formula for Combinations is: C(n,r) = 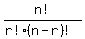 . So the first term of problem 9 would be C(5,2) = . So the first term of problem 9 would be C(5,2) = 
11. Order doesn't matter, that is to say it doesn't matter whether you choose the largest or the smallest nails first, or any other order. If order doesn't matter, use Combinations, so calculate: C(14,5) [14C5 in your notation].
12. This question asks about how many different orders, so order does matter. When order matters, use Permutations.
Calculate P(23,6).
23! and 14! are both huge numbers and a computational horror if you try to do it by hand. If you are using a Windows computer, there is a built-in calculator (look in Start-All Programs-Accessories). Once the calculator is running, choose the View menu and select Scientific. In the scientific mode, the calculator has an n! button. Just enter the number, then click the button. Otherwise, just use any standard scientific calculator and use the factorial function.
|
|
|