a) How many 4-digit numbers can be formed from the set A = {0,1,2,3,4,5,6}if there is no repetition?
Here is a sample choice:
3206
The number that goes where the 3 is can be any of 1, 2, 3, 4, 5, or 6.
0 cannot come first, so we can choose it any of 6 ways.
The number that goes where the 2 is can be 0 or any one of the
5 that was not chosen first. That's 6 ways.
The number that goes where the 0 can be any of the 5 that weren't
chosen first or second. That's 5 ways.
The number that goes where the 6 is can be any one of the 4 that
weren't chosen 1st, 2nd or 3rd. That's 4 ways.
The answer is 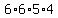 or
or 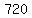 ways.
ways.
b) How many of the numbers in part a) are odd?
Here is a sample choic:
4361
Let's choose the 4th or last digit, where the 1 is,
first. It can only be 1, 3, or 5, since the number
must be odd. That's 3 ways.
Next choose the first digit. It cannot be 0 or the
digit that was chosen as the 4th digit. That's
5 ways.
Next choose the second digit. It can be 0 or any
digit that was not chosen as the 4th digit. That's
5 ways.
Finally choose the third digit. It can be any one of
the 4 remaining digits.
The answer is  or
or  ways.
ways.
c) How many of the numbers in part a) contain 3?
There are two ways to solve this.
First way.
A. The number of ways the 3 can come first.
Sample choice 3256:
There are 6 choices for the digit where the 2 is.
There are 5 choices for the digit where the 5 is.
There are 4 choices for the digit where the 6 is.
That's 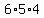 or
or  ways.
B. The number of ways the 3 can come 2nd.
Sample choice 4306:
There are 5 choices for the digit where the 4 is.
There are 5 choices for the digit where the 0 is.
There are 4 choices for the digit where the 6 is.
That's
ways.
B. The number of ways the 3 can come 2nd.
Sample choice 4306:
There are 5 choices for the digit where the 4 is.
There are 5 choices for the digit where the 0 is.
There are 4 choices for the digit where the 6 is.
That's 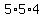 or
or  ways.
C. The number of ways the 3 can come 3rd.
This is also
ways.
C. The number of ways the 3 can come 3rd.
This is also  for we could just swap the
2nd and 3rd digits of B.
D. The number of ways the 3 can come 4th.
This is also
for we could just swap the
2nd and 3rd digits of B.
D. The number of ways the 3 can come 4th.
This is also  for we could just swap the
2nd and 4th digits of B.
That's a total of
for we could just swap the
2nd and 4th digits of B.
That's a total of 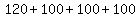 or
or  ways.
Second way.
Find the number which do not contain 3 and then subtract
from the total 720.
Now we are choosing from this set:
{0,1,2,4,5,6}
Here is a sample choice:
2046
The number that goes where the 2 is can be any of 1, 2, 4, 5, or 6.
0 cannot come first, so we can choose it any of 5 ways.
The number that goes where the 0 is can be 0 or any one of the
5 that was not chosen first. That's 5 ways.
The number that goes where the 4 is can be any of the 4 that weren't
chosen first or second. That's 4 ways.
The number that goes where the 6 is can be any one of the 3 that
weren't chosen 1st, 2nd or 3rd. That's 3 ways.
The answer is
ways.
Second way.
Find the number which do not contain 3 and then subtract
from the total 720.
Now we are choosing from this set:
{0,1,2,4,5,6}
Here is a sample choice:
2046
The number that goes where the 2 is can be any of 1, 2, 4, 5, or 6.
0 cannot come first, so we can choose it any of 5 ways.
The number that goes where the 0 is can be 0 or any one of the
5 that was not chosen first. That's 5 ways.
The number that goes where the 4 is can be any of the 4 that weren't
chosen first or second. That's 4 ways.
The number that goes where the 6 is can be any one of the 3 that
weren't chosen 1st, 2nd or 3rd. That's 3 ways.
The answer is 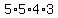 or
or  ways.
So we subtract these which don't contain 3 from the 720 and
get
ways.
So we subtract these which don't contain 3 from the 720 and
get 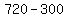 or
or  . This is the same answer
we got when doing it the other way.
. This is the same answer
we got when doing it the other way.
d) How many of the numbers in part a) are divisible by 5?
In order to be divisible by 5, the last digit can only be 0 or 5.
A. Cases when 0 comes last.
Here is a sample choice:
5240
There are 6 choices for the digit where the 5 is.
There are 5 choices for the digit where the 2 is.
There are 4 choices for the digit where the 4 is.
That's 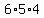 or
or  ways.
B. Cases when 5 comes last.
Here is a sample choice:
3625
There are 5 choices for the digit where the 3 is,
as it cannot be 0.
There are 5 choices for the digit where the 6 is.
There are 4 choices for the digit where the 2 is.
That's
ways.
B. Cases when 5 comes last.
Here is a sample choice:
3625
There are 5 choices for the digit where the 3 is,
as it cannot be 0.
There are 5 choices for the digit where the 6 is.
There are 4 choices for the digit where the 2 is.
That's 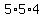 or
or  ways.
The total from A and B is
ways.
The total from A and B is
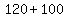 or
or 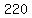 ways.
Edwin
ways.
Edwin