Question 159547: can you explain, how to get the combination formulas? and what's the different between permutation and combination?
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! permutation is an ordered set meaning AB is not equal to BA because A coming first and B coming next is not the same as B coming first and A coming next.
--------------------------
a combination is an unordered set meaning AB is equal to BA because it doesn't matter which comes first.
---------------------------
formula for permutation is 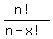
--------------------------
formula for combination is 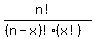
--------------------------
n stands for the total number of items in the set
x stands for the subset that you want to create from it.
---------------------------
to show you what this means we'll use a simple example:
-----
you have 4 letters in the set.
this makes n = 4
let the letters be A, B, C, and D.
----
you want to create a subset of 3 of these letters.
this makes x = 3
in the first subset, order is important, i.e. ABC does not equal ACB.
in the second subset, order is not important, i.e. ABC equals ACB or BAC or BCA or CAB or CBA.
---
we'll do permutation first.
formula becomes 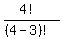 which is the same as which is the same as  which becomes 24. which becomes 24.
this means there are 24 possible different arrangements you can make if you assume that the order in the arrangement is important.
to prove this, list all possible permutations.
starting with A you can have
ABC
ABD
ACB
ACD
ADB
ADC
starting with B you can have
BAC
BAD
BCA
BCD
BDA
BDC
starting with C you can have
CAB
CAD
CBA
CBD
CDA
CDB
starting with D you can have
DAB
DAC
DBA
DBC
DCA
DCB
---------------------------
as you can see this is a total of 24 arrangements where order is important.
---------------------------
we'll do combinations next.
formula becomes  which becomes which becomes 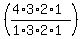 which becomes 4. which becomes 4.
---------------------------
if this formula is correct there should only be 4 possible combinations that can be made as long as order not important.
---------------------------
listing them gets
ABC
ABD
ACD
BCD
---------------------------
everything else should be a combination of the same letters in different order.
to test, go down the list of permutations and take out anything that has the 3 letters listed in each of these possible combinations in them but in different order.
i'll list the permutations below and indicate the ones that can be removed.
-----------------------
starting with A you can have
ABC
ABD
ACB ***
ACD
ADB ***
ADC ***
starting with B you can have
BAC ***
BAD ***
BCA ***
BCD
BDA ***
BDC ***
starting with C you can have
CAB ***
CAD ***
CBA ***
CBD ***
CDA ***
CDB ***
starting with D you can have
DAB ***
DAC ***
DBA ***
DBC ***
DCA ***
DCB ***
---------------------------
you are left with 4 that contain unique representations of the letters A,B,C,D without regard to order.
|
|
|