Question 136380: how do you find the vertical and horizontal asymptotes, the hole and RD and graph the problem: y= 3/(x-2)(x+2)
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! Vertical asymptotes are vertical lines of the form  where  is any value that makes the denominator of the rational expression go to zero. The given rational expression has two such values, so you will have two vertical asymptotes.
Horizontal asymptotes are horizontal lines of the form  . For any given rational expression there is either one horizontal asymptote or none.
Compare the degree of the polynomial in the numerator to the degree of the polynomial in the denominator.
If the degree of the denominator polynomial is larger, then there is a horizontal asymptote at  .
If the degrees of the denominator and numerator are equal, there is a horizontal asymptote at  where p is the lead coefficient (the coefficient of the highest order term in the polynomial) on the numerator polynomial, and q is the lead coefficient on the denominator polynomial.
If the degree of the denominator polynomial is smaller, then there is no horizontal asymptote. There is, however, a slant or oblique asymptote (a straight line if the degrees differ by 1) that is found by taking the quotient (excluding the remainder) of the polynomial long division of the denominator into the numerator.
Hint: The degree of a single term polynomial consisting only of a constant value is zero.
Holes:
Holes are values of the variable where both numerator and denominator are zero. So, is it possible for the numerator of your expression to ever be zero?
I have no idea what an 'RD' is, and can't seem to locate the term associated with the process of graphing rational functions anywhere on the web. Please define, and perhaps I can help.
You might also want to examine the zeros of the function. The zeros of the function are values of x for which f(x)=0. For a rational function, this is done by setting the numerator equal to zero and solving the resultant equation and excluding any value that would also make the denominator zero (See discussion on "holes"). This is because  if and only if  and  .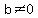
Your graph should resemble this: (Ignore the vertical(sort of) lines that are an idiosyncracy of the graphing system on this site)
|
|
|
