Question 1210229: Find the number of subsets of
S = \{1, 3, 8, 17, 30, 36, 47, 58\},
so that the sum of the elements in the subset is less than 20. (Note that for the empty subset, we take the sum of the elements as 0.)
Found 3 solutions by CPhill, ikleyn, greenestamps:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Solution:
We are asked to find the number of subsets of $S = \{1, 3, 8, 17, 30, 36, 47, 58\}$ such that the sum of the elements in the subset is less than 20.
We can consider each element of $S$ and decide whether to include it in a subset. Since the elements are sorted, we can proceed by considering smaller elements first.
Case 1: Subsets with 0 elements
The only subset with 0 elements is the empty set, $\emptyset$. The sum of its elements is 0, which is less than 20.
Number of subsets = 1 ($\emptyset$)
Case 2: Subsets with 1 element
The subsets with 1 element are $\{1\}, \{3\}, \{8\}, \{17\}, \{30\}, \{36\}, \{47\}, \{58\}$.
The sums of the elements are 1, 3, 8, 17, 30, 36, 47, 58.
The sums less than 20 are 1, 3, 8, 17.
The subsets are $\{1\}, \{3\}, \{8\}, \{17\}$.
Number of subsets = 4
Case 3: Subsets with 2 elements
We consider pairs of distinct elements from $S$ and check if their sum is less than 20.
Pairs involving 1: $\{1, 3\} \rightarrow 4$, $\{1, 8\} \rightarrow 9$, $\{1, 17\} \rightarrow 18$. (3 subsets)
Pairs involving 3 (excluding pairs with 1): $\{3, 8\} \rightarrow 11$, $\{3, 17\} \rightarrow 20$ (sum not less than 20). (1 subset)
Pairs involving 8 (excluding pairs with 1 and 3): $\{8, 17\} \rightarrow 25$ (sum not less than 20). (0 subsets)
The 2-element subsets with a sum less than 20 are $\{1, 3\}, \{1, 8\}, \{1, 17\}, \{3, 8\}$.
Number of subsets = 4
Case 4: Subsets with 3 elements
We consider triplets of distinct elements from $S$ and check if their sum is less than 20.
Triplets involving 1 and 3: $\{1, 3, 8\} \rightarrow 12$, $\{1, 3, 17\} \rightarrow 21$ (sum not less than 20). (1 subset)
Triplets involving 1 and 8 (excluding triplets with 3): $\{1, 8, 17\} \rightarrow 26$ (sum not less than 20). (0 subsets)
The 3-element subset with a sum less than 20 is $\{1, 3, 8\}$.
Number of subsets = 1
Case 5: Subsets with 4 or more elements
The smallest 4 elements of $S$ are 1, 3, 8, 17. Their sum is $1 + 3 + 8 + 17 = 29$, which is not less than 20. Therefore, there are no subsets with 4 or more elements whose sum is less than 20.
Total number of subsets with a sum less than 20 is the sum of the number of subsets from each case:
Total = (Number of 0-element subsets) + (Number of 1-element subsets) + (Number of 2-element subsets) + (Number of 3-element subsets)
Total = $1 + 4 + 4 + 1 = 10$
Final Answer: The final answer is $\boxed{10}$
Answer by ikleyn(52777)  (Show Source):
You can put this solution on YOUR website! .
Find the number of subsets of
S = {1, 3, 8, 17, 30, 36, 47, 58},
so that the sum of the elements in the subset is less than 20.
(Note that for the empty subset, we take the sum of the elements as 0.)
~~~~~~~~~~~~~~~~~~~~~~~
Looking into the given set, we see that all numbers 30, 36, 47, 58 can be excluded
from consideration, since each of them is just greater than 20.
So, the original set of 8 numbers can be reduced to the set of 4 numbers {1, 3, 8, 17}.
For this set of 4 numbers, the number of all its subsets is 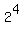 = 16.
But not all of these 16 subsets fit the condition.
We should exclude the subsets that produce the sum 20 or greater.
So, the subsets to exclude are these 6 subsets
{1, 3, 8, 17}, {1, 3, 17}, {1, 8, 17}, {3, 8, 17}, {3,17}, {8,17}.
The rest of the subsets, 16 - 6 = 10, fit the condition.
ANSWER. There are 10 subsets that fit the condition.
Solved.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
Since the elements 30, 36, 47, and 58 are each alone greater than 20, the only elements we need to consider are 1, 3, 8, and 17.
subsets with 0 elements: { }
Number of subsets with 0 elements and a sum of less than 20: 1
subsets with 1 element: {1}, {3}, {8}, {17}
Number of subsets with 1 element and a sum of less than 20: 4
subsets with 2 elements: {1,3}, {1,8}, {1,17}; {3,8}
Number of subsets with 2 elements and a sum of less than 20: 4
subsets with 3 elements: {1,3,8}
Number of subsets with 3 elements and a sum of less than 20: 1
Total number of subsets with a sum of less than 20: 1+4+4+1 = 10
ANSWER: 10
|
|
|
