Question 1210194: At a meeting, two scientists, two mathematicians, two historians, and two artists are to be seated around a circular table. In how many ways can they be seated so that all four pairs of people from the same discipline are seated together?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step.
**1. Treat Each Pair as a Unit**
* Since each pair of people from the same discipline must sit together, we can treat each pair as a single unit.
* We have 4 units: scientists (S), mathematicians (M), historians (H), and artists (A).
**2. Arrange the Units Around the Circular Table**
* The number of ways to arrange n distinct objects in a circle is (n-1)!.
* In this case, we have 4 units, so the number of ways to arrange them around the circular table is (4-1)! = 3! = 3 * 2 * 1 = 6.
**3. Arrange the People Within Each Pair**
* Each pair of people can be arranged in 2! = 2 ways.
* Scientists: 2! = 2 ways
* Mathematicians: 2! = 2 ways
* Historians: 2! = 2 ways
* Artists: 2! = 2 ways
**4. Multiply the Arrangements**
* To get the total number of arrangements, we multiply the number of ways to arrange the units around the table by the number of ways to arrange the people within each pair.
* Total arrangements = 3! * 2! * 2! * 2! * 2!
* Total arrangements = 6 * 2 * 2 * 2 * 2 = 6 * 16 = 96
**Therefore, there are 96 ways to seat the people so that all four pairs of people from the same discipline are seated together.**
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
At a meeting, two scientists, two mathematicians, two historians, and two artists are to be seated around a circular table.
In how many ways can they be seated so that all four pairs of people from the same discipline are seated together?
~~~~~~~~~~~~~~~~~~~~~~~
Since you came with pairs of persons around a round table, it means (at the normal teaching process)
that you are just familiar with the basic cases for such problems.
So, I will not repeat the basics, but will simply give a short form solution.
In this problem, we have 4 pairs as the units/items.
4 items can be placed around a circle in (4-1)! = 3! = 6 different way (circular permutations).
In addition, one permutation is possible inside each pair.
It gives, in total, 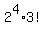 = 16*6 = 96 different circular placements in this problem. ANSWER
Solved.
|
|
|
