Question 1210186: Find the number of positive integers that are divisors of at least one of 6^{6}, 10^{10}, 15^{15}, and 30^{30}.
Found 6 solutions by CPhill, ikleyn, greenestamps, mccravyedwin, Edwin McCravy, AnlytcPhil:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step.
**1. Prime Factorization**
* $6^6 = (2 \cdot 3)^6 = 2^6 \cdot 3^6$
* $10^{10} = (2 \cdot 5)^{10} = 2^{10} \cdot 5^{10}$
* $15^{15} = (3 \cdot 5)^{15} = 3^{15} \cdot 5^{15}$
* $30^{30} = (2 \cdot 3 \cdot 5)^{30} = 2^{30} \cdot 3^{30} \cdot 5^{30}$
**2. Understanding Divisors**
A divisor of any of these numbers will be of the form $2^a \cdot 3^b \cdot 5^c$, where:
* $0 \le a \le 30$ (since $2^{30}$ is the highest power of 2)
* $0 \le b \le 30$ (since $3^{30}$ is the highest power of 3)
* $0 \le c \le 30$ (since $5^{30}$ is the highest power of 5)
**3. Total Possible Divisors**
If we consider all possible combinations of a, b, and c, we have:
* 31 choices for a (0 to 30)
* 31 choices for b (0 to 30)
* 31 choices for c (0 to 30)
Therefore, the total number of possible divisors is $31 \cdot 31 \cdot 31 = 31^3 = 29791$.
**4. Inclusion-Exclusion Principle**
We need to find the number of divisors that are divisors of *at least one* of the given numbers. We can use the inclusion-exclusion principle.
* Let A be the set of divisors of $6^6$.
* Let B be the set of divisors of $10^{10}$.
* Let C be the set of divisors of $15^{15}$.
* Let D be the set of divisors of $30^{30}$.
We want to find $|A \cup B \cup C \cup D|$.
Since $30^{30}$ contains all prime factors of the other 3, any divisor of $6^6$, $10^{10}$, or $15^{15}$ will also be a divisor of $30^{30}$.
Therefore, $|A \cup B \cup C \cup D| = |D|$.
* $|D| = (30+1)(30+1)(30+1) = 31^3 = 29791$
**5. Final Answer**
The number of positive integers that are divisors of at least one of the given numbers is $31^3 = 29791$.
**Therefore, the answer is 29791.**
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the number of positive integers that are divisors of at least one of 6^{6}, 10^{10}, 15^{15}, and 30^{30}.
~~~~~~~~~~~~~~~~~~~~~~~~
Notice that all three numbers  , ,  and and 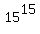 are divisors of the number are divisors of the number 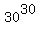 .
Therefore, you can simplify the problem's formulation: you ONLY need to find the number of divisors of .
Therefore, you can simplify the problem's formulation: you ONLY need to find the number of divisors of 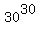 .
The prime decomposition for 30 is 30 = 2*3*5.
So, .
The prime decomposition for 30 is 30 = 2*3*5.
So, 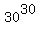 = = 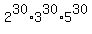 .
For this number, its divisors are all
1, 2, .
For this number, its divisors are all
1, 2, 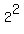 , . . . , , . . . , 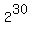 (31 divisor),
1, 3, (31 divisor),
1, 3,  , . . . , , . . . , 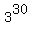 (31 divisor),
1, 5, (31 divisor),
1, 5,  , . . . , , . . . , 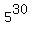 (31 divisor)
and all of their products.
The number of all their distinct products is 31*31*31 = (31 divisor)
and all of their products.
The number of all their distinct products is 31*31*31 = 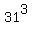 = 29791.
It is the ANSWER to the problem's question. = 29791.
It is the ANSWER to the problem's question.
Solved.
I wrote this my post after @CPhill to provide the most simple straightforward solution/explanation
and to remove all unnecessary complications from the post by @CPhill.
/////////////////////////////
Edwin, I think it was very good from your side to make this editing in your post
and to exclude/ (to remove) your unjustified insinuations against me from the original version.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Note that 6^6, 10^10, and 15^15 are all factors of 30^30. It is therefore only necessary to find the number of positive integers that are factors of 30^30.
The standard method for determining the number of factors of a given integer N is
(1) find the prime factorization of N;
(2) add 1 to each exponent in the prime factorization; and
(3) multiply the numbers from step (2)
The prime factorization of 30 is 2*3*5, so the prime factorization of 30^30 is (2^30)(3^30)(5^30).
The number of factors of 30^30 is (30+1)(30+1)(30+1) = 31^3 = 29791
ANSWER: 29791
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I think everybody has it right now. There has been some editing going on.
 .
All factors have to be of the form .
All factors have to be of the form 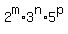 where there are 31 choices for each ordered triple of exponents (m,n,p),
namely 0,1,2,...30.
Edwin
where there are 31 choices for each ordered triple of exponents (m,n,p),
namely 0,1,2,...30.
Edwin
|
|
|