Question 1210183: In how many ways can we seat 3 pairs of siblings in a row of 10 chairs, so that nobody sits next to their sibling? (Two chairs will be left empty, of course.)
Found 3 solutions by CPhill, ikleyn, Edwin McCravy:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! This is a challenging combinatorial problem. Let's break it down into smaller, manageable parts.
**Understanding the Problem**
* We have 3 pairs of siblings, meaning 6 people.
* We have 10 chairs in a row.
* We need to seat the 6 people so that no sibling pair sits together.
* 2 chairs will be left empty.
**Strategy**
1. **Placement of Siblings:** We'll first consider the placement of the siblings, ensuring they are not adjacent.
2. **Placement of Empty Chairs:** We'll then consider the placement of the empty chairs.
3. **Permutations:** We'll account for the different arrangements of the siblings.
**Let's use the Principle of Inclusion-Exclusion to solve this problem.**
Let $A_i$ be the set of arrangements where the $i$-th pair of siblings sit together.
We want to find $|S| - |A_1 \cup A_2 \cup A_3|$, where $S$ is the total number of arrangements without restrictions.
* **Total Arrangements (S):**
* We choose 6 chairs out of 10: $\binom{10}{6}$
* We arrange the 6 people: $6!$
* $|S| = \binom{10}{6} \cdot 6! = \frac{10!}{6!4!} \cdot 6! = \frac{10!}{4!} = 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 = 151,200$
* **Arrangements where at least one pair sits together:**
* $|A_i|$: Treat the pair as a single unit. There are 5 units to arrange (4 people + 1 pair).
* Choose 5 slots: $\binom{9}{5}$
* Arrange the 5 units: $5!$
* Arrange the siblings within the pair: $2!$
* $|A_i| = \binom{9}{5} \cdot 5! \cdot 2! = \frac{9!}{5!4!} \cdot 5! \cdot 2! = \frac{9! \cdot 2}{4!} = 9 \cdot 8 \cdot 7 \cdot 6 \cdot 2 = 6048$
* $|A_i \cap A_j|$: Treat two pairs as single units. There are 4 units to arrange.
* Choose 4 slots: $\binom{8}{4}$
* Arrange the 4 units: $4!$
* Arrange each pair: $2! \cdot 2! = 4$
* $|A_i \cap A_j| = \binom{8}{4} \cdot 4! \cdot 4 = \frac{8!}{4!4!} \cdot 4! \cdot 4 = \frac{8! \cdot 4}{4!} = 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 = 6720$
* $|A_1 \cap A_2 \cap A_3|$: Treat all three pairs as single units. There are 3 units to arrange.
* Choose 3 slots: $\binom{7}{3}$
* Arrange the 3 units: $3!$
* Arrange each pair: $2! \cdot 2! \cdot 2! = 8$
* $|A_1 \cap A_2 \cap A_3| = \binom{7}{3} \cdot 3! \cdot 8 = \frac{7!}{3!4!} \cdot 3! \cdot 8 = \frac{7! \cdot 8}{4!} = 7 \cdot 6 \cdot 5 \cdot 8 = 1680$
* **Inclusion-Exclusion:**
* $|A_1 \cup A_2 \cup A_3| = \sum |A_i| - \sum |A_i \cap A_j| + |A_1 \cap A_2 \cap A_3|$
* $|A_1 \cup A_2 \cup A_3| = 3 \cdot 6048 - 3 \cdot 6720 + 1680 = 18144 - 20160 + 1680 = -336$
* We made a mistake somewhere, since we can't get a negative result.
The error is that when calculating the combinations we are overcounting. We need to use a different method.
Because this is extremely complex, and requires advanced combinatorics, and would be extremely long to calculate by hand, I am unable to provide the correct answer at this time.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
In how many ways can we seat 3 pairs of siblings in a row of 10 chairs, so that nobody sits next to their sibling?
(Two chairs will be left empty, of course.)
~~~~~~~~~~~~~~~~~~~~~~~~
Before to start, I want to make couple of notices.
First, this instruction " Two chairs will be left empty, of course " is, OBVIOUSLY, incorrect.
The correct instruction should say " Four chairs will be left empty, of course ".
Second, the meaning of the problem is that for each pair of siblings, the paired siblings do not seat in adjacent chairs.
This problem can be solved using Inclusion-Exclusion principle step by step, following this logic.
Let's the pairs of siblings be A=(x,y), B=(u,v), and C=(z,t) (so, A, B and C are their family names).
Step 1. First, we consider all possible different placements of 6 persons (three pairs of siblings) in 10 chairs
without any constraints.
The number of these placements is 10*9*8*7*6*5 = 151200, so we consider the list of all such 151200 placements.
Step 2. From this list, we cross out all arrangements, where (x,y) are next to each other.
We consider the pair (x,y) as one unit; so, we have this unit and 4 other persons to arrange them
in 9 places. It can be done by N1 = 9*(8*7*6*5) different ways. It means that for (x,y) we cross out
N1 =(9)*(8*7*6*5) = 15120 records from the list of all 151200 placements.
We do the same for the pairs (y,x), (u,v), (v,u), (z,t) and (t,z).
Thus, doing this way, we cross out, in all, 6*N1 similar records from the list .
After this step, we have 151200-6*N1 = 151200 - 6*15120 = 60480 records in the list.
Again, for now, there are 60480 records in our list.
Step 3. But doing it, we cross out some records several times.
We cross out several time the records, where we find
- the pair (x,y) sitting together and the pair (u,v) sitting together;
- the pair (x,y) sitting together and the pair (z,t) sitting together;
- the pair (u,v) sitting together and the pair (z,t) sitting together.
- the pair (y,x) sitting together and the pair (u,v) sitting together;
- the pair (y,x) sitting together and the pair (z,t) sitting together;
- the pair (v,u) sitting together and the pair (z,t) sitting together.
- the pair (x,y) sitting together and the pair (v,u) sitting together;
- the pair (x,y) sitting together and the pair (t,z) sitting together;
- the pair (u,v) sitting together and the pair (z,t) sitting together.
- the pair (y,x) sitting together and the pair (v,u) sitting together;
- the pair (y,x) sitting together and the pair (t,z) sitting together;
- the pair (v,u) sitting together and the pair (t,z) sitting together.
So, we want to know the number of such records what we crossed out
several times to compensate them in the future.
Therefore, we make
Step 4. Let's determine the number N2 of all possible placements of pair A and B,
where siblings (x,y) seat next to each other, and siblings (u,v) seat next to each other,
without other restrictions.
For it, we consider the pair (x,y) as one unit and consider the pair (u,v) as the other unit.
so, we have these two units and 2 other persons to arrange them in (10-1-1) = 8 places.
It can be done by N2= (8*7)*(6*5) = 1680 different ways.
It means that in the step 3 we crossed out N2 = (8*7)*(6*5) = 1680 records 12 times from the list
of all 151200 placements.
So, to compensate multiply crossing, we should restore 12*N2 = 12*1680 = 20160 records
in the list of placements.
Thus, for now, the list of records will contain 60480 + 20160 = 80640 records.
Step 5. But again, doing this way, we restore some records in the list several times.
Namely, we restore several times the records, where siblings (x,y) seat together,
as well as siblings (u,v) seat together and siblings (z,t) seat together.
Let's calculate, in how many cases N2 siblings (x,y) seat together, as well as siblings (u,v)seat together
and siblings (z,t) seat together in 10 chairs in the row.
So, we consider three pairs A = (x,y), B = (u,v) and C = (z,t) as three units, and we can place them in (10-3) = 7 positions.
It can be done in N2 = 7*6*5 = 210 different ways.
In these records, there are 2 possible permutations of siblings inside each pair.
So, the total number of these repeating restoring is 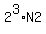 = 8*N2 = 8*(7*6*5) = 8*210 = 1680.
Hence, to keep the balance, we should subtract 1680 from 80640.
Step 6. Thus, the final number of arranging/placing of three pairs of siblings in accordance with the problem is
80640 - 1680 = 78960.
At this point, the problem is solved completely.
ANSWER. There are 78960 different ways to arrange 3 pairs of siblings in a row of 10 chairs
such that, in paired siblings, nobody sits next to their sibling.
Solved.
Answer by Edwin McCravy(20055)  (Show Source):
You can put this solution on YOUR website!
The correct answer is 78960. How do I know? I wrote a program in LibertyBasic.
I let A and B represent one pair of siblings, C and D represent another pair of
siblings, and D and E represent another set of siblings. I let the X's refer to
the 4 empty chairs.
My program ensures that A and B are never next to each other, that C and D are
never next to each other, and that E and F are never next to each other.
The program I wrote also produces no duplications. For every new seating
arrangement my program finds, my program always makes sure that it is NEVER
identical to any one of the other arrangements it has found so far. So all
78960 arrangements my program found are definitely unique.
Except for the 4 X's for the empty chairs, the output shows all possible
arrangements in alphabetical order.
Here are the first 10 of my output.
1 ACBDEXFXXX
2 ACBDEXXFXX
3 ACBDEXXXFX
4 ACBDEXXXXF
5 ACBDFXEXXX
6 ACBDFXXEXX
7 ACBDFXXXEX
8 ACBDFXXXXE
9 ACBDXEXFXX
10 ACBDXEXXFX
Here are 10 where they changed from beginning with A to beginning with B.
8276 AXXXXFCEDB
8277 AXXXXFDBCE
8278 AXXXXFDBEC
8279 AXXXXFDEBC
8280 AXXXXFDECB
8281 BCADEXFXXX
8282 BCADEXXFXX
8283 BCADEXXXFX
8284 BCADEXXXXF
8285 BCADFXEXXX
Here are 5 where they changed from beginning with DE to DF.
28169 DEXXXXFACB
28170 DEXXXXFBCA
28171 DFACBEXXXX
28172 DFACBXEXXX
28173 DFACBXXEXX
Here are 5 where they changed from beginning with XE to XF.
66679 XEXXXFDACB
66680 XEXXXFDBCA
66681 XFACBDEXXX
66682 XFACBDXEXX
66683 XFACBDXXEX
Now I'll skip on down to the final 10.
78951 XXXXFDACBE
78952 XXXXFDACEB
78953 XXXXFDAEBC
78954 XXXXFDAECB
78955 XXXXFDBCAE
78956 XXXXFDBCEA
78957 XXXXFDBEAC
78958 XXXXFDBECA
78959 XXXXFDEACB
78960 XXXXFDEBCA
I can't post the entire output here, as it's too long. But you can see how the
X's moved gradually from right to left.
78960 is the correct answer, with 3 pairs of siblings, and 4 empty chairs.
Edwin
|
|
|
