Question 1210171: Find the number of ways of placing three As, three Bs, and three Cs in a 3 \times 3 grid, so that every square contains one letter, and each diagonal contains one A, one B, and one C.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! We are asked to count the number of ways to place **three A's, three B's, and three C's** in a **3×3 grid** such that:
- Every square contains exactly one letter.
- Each **row** and **column** ends up with 3 letters total (since the grid is filled).
- **Each diagonal** (main and anti-diagonal) must contain exactly **one A, one B, and one C**.
---
### Step 1: Total number of arrangements without the diagonal condition
We need to place 3 A’s, 3 B’s, and 3 C’s into 9 positions. This is a classic **multinomial coefficient**:
\[
\frac{9!}{3! \cdot 3! \cdot 3!} = \frac{362880}{6 \cdot 6 \cdot 6} = \frac{362880}{216} = 1680
\]
So there are **1680** total ways to fill the grid with 3 A’s, 3 B’s, and 3 C’s.
---
### Step 2: Apply the diagonal condition
We must now count **only those** of the 1680 arrangements in which:
- The **main diagonal** (top-left to bottom-right) contains one A, one B, and one C.
- The **anti-diagonal** (top-right to bottom-left) also contains one A, one B, and one C.
Let’s define the positions in the grid like this:
```
(1,1) (1,2) (1,3)
(2,1) (2,2) (2,3)
(3,1) (3,2) (3,3)
```
The **main diagonal** is: (1,1), (2,2), (3,3)
The **anti-diagonal** is: (1,3), (2,2), (3,1)
Note that the **center square (2,2)** is on **both diagonals**.
---
So the union of the two diagonals has 5 distinct squares:
- Main: (1,1), (2,2), (3,3)
- Anti: (1,3), (2,2), (3,1)
=> Union: **(1,1), (2,2), (3,3), (1,3), (3,1)**
This gives us **5 positions**, with **(2,2)** counted once (in both diagonals).
---
We want these two diagonals (i.e., the five cells) to include:
- Each of A, B, and C **exactly once** in each diagonal.
Let’s approach it step by step.
---
### Step 3: Count the valid diagonal assignments
We'll now count the number of ways to assign letters to the **5 diagonal positions**, so that:
- (1,1), (2,2), (3,3) have one A, one B, one C (i.e., main diagonal is a permutation of A, B, C)
- (1,3), (2,2), (3,1) also have one A, one B, one C (anti-diagonal is a permutation of A, B, C)
Key insight: The **center** cell (2,2) is in **both** diagonals, so its letter is shared.
Let’s choose the letter for the **center cell (2,2)** first.
We have **3 choices**: A, B, or C.
For each such choice:
- The main diagonal now needs to use the other two letters (excluding the center), and arrange them in the remaining two diagonal spots: (1,1) and (3,3).
- Similarly, the anti-diagonal uses the same idea for (1,3) and (3,1).
So for each choice of letter at (2,2), the number of ways to assign letters to the rest of the diagonals is:
\[
(\text{ways to fill the other 2 positions in main diagonal}) \times (\text{ways to fill the other 2 in anti-diagonal}) = 2! \times 2! = 2 \times 2 = 4
\]
So total number of valid ways to fill the **5 diagonal squares** is:
\[
3 \text{ (choices for center)} \times 4 = 12
\]
---
### Step 4: Fill the remaining 4 squares
Now we’ve filled 5 of the 9 squares, each with one letter (from A, B, or C). We used 5 letters total, one per square.
So we have 4 squares left, and **we need to use up the remaining letters** so that each letter (A, B, C) appears exactly 3 times.
Let’s do the math:
We used:
- 1 A, 1 B, 1 C in each diagonal (so 2 of each total),
- But the center letter was **shared**, so total count so far is:
- The center letter appears once.
- The other two letters appear twice each (once in each diagonal).
Let’s break it down depending on the center letter. For example:
- Suppose the center is A.
- Then main diagonal: A (center), B, C → uses 1 B, 1 C
- Anti-diagonal: A (same center), B, C → uses another 1 B, 1 C
So we’ve placed:
- A: 1 time
- B: 2 times
- C: 2 times
So we have:
- 2 more A’s to place
- 1 more B
- 1 more C
Total of 4 letters to place in the 4 remaining squares.
This pattern is the same no matter what the center letter is — we always end up needing to place **2 of one letter** (the center one) and **1 of each of the other two**.
So for each of the 12 diagonal configurations, the remaining 4 letters to place are fixed, and we need to count the number of ways to assign them to the 4 leftover squares.
We are placing 4 letters: one letter appears twice, the others once each.
So the number of arrangements is:
\[
\frac{4!}{2! \cdot 1! \cdot 1!} = 12
\]
---
### Step 5: Multiply it all together
- 12 valid ways to assign letters to the 5 diagonal squares
- For each of those, 12 ways to fill the other 4 squares
So total number of valid arrangements is:
\[
12 \times 12 = \boxed{144}
\]
---
### ✅ Final Answer:
\[
\boxed{144}
\]
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
Find the number of ways of placing three As, three Bs, and three Cs in a 3x3 grid,
so that every square contains one letter, and each diagonal contains one A, one B, and one C.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, three As are indistinguishable, as well as three Bs and three Cs.
Therefore, the subject of consideration are not permutations - the subject of
consideration are distinguishable arrangements.
Looking at the diagonal cells (1,1), (2,2), (3,3), three different letters A, B and C can be
placed there in 6 different distinguishable ways.
(1) Let assume that the letter in upper left corner (1,0) is A
and that the letter in central cell (2,2) is B.
Then the letter in the cell (3,3) is C inevitably.
In the cell (3,1) we have choice of two letters A or C
Then in the cell (1,3) we must place C or A oppositely, with no choice.
The remaining cells (1,2), (2,1), (2,3) and (3,2) we can fill with remaining letters,
with no constraints.
The remaining letters are A, two Bs and C.
This 4 letters can be placed in the remaining 4 cells by 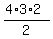 = 12 different distinguishable ways .
Thus, starting from A and B in (1,1) and (2,2), we have 2*12 = 24 choices for placing the other letters.
(2) Let assume that the letter in upper left corner (1,0) is B
and that the letter in central cell (2,2) is A.
Then, reasoning by the same way, we will have 24 different distinguishable choices
in placing all other letter.
(3) Let assume that the letter in upper left corner (1,0) is A
and that the letter in central cell (2,2) is C.
Then, reasoning by the same way, we will have 24 different distinguishable choices
in placing all other letter.
(4) Let assume that the letter in upper left corner (1,0) is C
and that the letter in central cell (2,2) is A.
Then, reasoning by the same way, we will have 24 different distinguishable choices
in placing all other letter.
(5) Let assume that the letter in upper left corner (1,0) is B
and that the letter in central cell (2,2) is c.
Then, reasoning by the same way, we will have 24 different distinguishable choices
in placing all other letter.
(6) Let assume that the letter in upper left corner (1,0) is C
and that the letter in central cell (2,2) is B.
Then, reasoning by the same way, we will have 24 different distinguishable choices
in placing all other letter.
Thus we analyzed all 6 possible placements of letters on the major diagonal,
and we saw that each such placing creates 24 different placing for the rest of letters.
Therefore, the total number of all possible distinguishable placing (arrangements)
of the letters in this problem is
6 * 24 = 144. <<<---=== ANSWER
Solved.
|
|
|
