Question 1209003: Suppose we want to choose 6 letters, without replacement, from 8 distinct letters.
How many ways can this be done, if the order of the choices does not matter?
How many ways can this be done, if the order of the choices matters?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
Suppose we want to choose 6 letters, without replacement, from 8 distinct letters.
(a) How many ways can this be done, if the order of the choices does not matter?
(b) How many ways can this be done, if the order of the choices matters?
~~~~~~~~~~~~~~~~~~~~~~~
(a) If the order does not matter, then the question is about combinations.
The number of choices is the number of combinations of 8 distinct letters taken 6 at a time
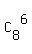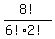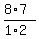 =  =  = 4*7 = 28.
(b) If the order does matter, then the question is about permutations.
1st letter can be any of 8 letters, giving 8 options.
2nd letter can be any of 7 remaining letters, giving 7 options.
3rd letter can be any of 6 remaining letters, giving 6 options.
4th letter can be any of 5 remaining letters, giving 5 options.
5th letter can be any of 4 remaining letters, giving 4 options.
6th letter can be any of 3 remaining letters, giving 3 options.
The total number of possible choices in this case is 8*7*6*5*4*3 =20160.
Solved, with complete explanations.
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
This might be a bit strange, but I'll address the "order matters" portion first.
There are n = 8 letters and r = 6 slots to fill.
We have 8 choices for the first slot, then 7 for the next, and so on until reaching n-r+1 = 8-6+1 = 3 choices for the 6th slot.
Multiplying out these values gives: (8*7*6)*(5*4*3) = 20160 different permutations where order matters.
Another way to reach this value is to use the nPr permutation formula.
nPr = (n!)/( (n-r)! )
which I'll let the student handle the scratch work if s/he chooses this route.
The exclamation mark indicates a factorial.
-----------
Now onto the "order doesn't matter" portion.
For any group of 6 items, we have 6! = 6*5*4*3*2*1 = 720 ways to rearrange said group.
This means that the previous value we found (20160) is too large by a factor of 720 if order doesn't matter.
We'll divide the permutation value over r! = 6! = 720 to find the combination value.
A very useful formula is
nCr = (nPr)/(r!)
which is a way to connect permutations to combinations.
There are 20160/720 = 28 combinations.
This value can be found by looking at Pascal's Triangle.
Since n = 8, we start with the row "1,8,..."
r = 0 is the starting index and refers to the left-most value in this row. Increment r by 1 each time you move to the right. Once reaching r = 6, you should arrive at 28 in Pascal's Triangle.
Or if you wanted you can use this nCr formula
nCr = (n!)/( r!*(n-r)! )
I'll let the student handle the scratch work if s/he chooses this route.
Notice the presence of n! up top and (n-r)! down below; both of which are found in the nPr formula.
So that can help explain why nCr = (nPr)/(r!) is true.
--------------------------------------------------------------------------
--------------------------------------------------------------------------
Answers:
How many ways can this be done, if...
Order doesn't matter? 28
Order does matter? 20160
|
|
|
