Question 1208703: A standard six-sided die is rolled $8$ times. You are told that among the rolls, there was one $1$, two $2$'s, four $3$'s, and one $4$. How many possible sequences of rolls could there have been? (For example, $2,$ $1,$ $3,$ $3,$ $3,$ $2,$ $3,$ $4$ is one possible sequence.)
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
A standard six-sided die is rolled 8 times. You are told that among the rolls, there was one 1, two 2's, four 3's, and one 4.
How many possible sequences of rolls could there have been? (For example, 2, 1, 3, 3, 3, 2, 3, 4 is one possible sequence.)
~~~~~~~~~~~~~~~~
There are 8 possible positions to place the given outcomes of 8 rolls.
The unique "1" can be placed to any of 8 positions.
The two 2's can be placed to any 2 of remaining 8-1 = 7 positions.
The four 3's can be placed to any 4 of of remaining 7-2 = 5 positions.
The last "4" should be placed to unique remaining 5-4 = 1 position, with no choice.
The total number of different placements is 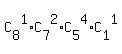 =  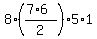= 8*21*5*1 = 840.
ANSWER. The total number of different placements is 840.
Solved.
We use combinations, since the order of outcomes inside each set of co-named outcomes does not matter.
|
|
|
