Question 1208392: On a library shelf there are 5 different science books and 4 different math books. Find the number of ways to arrange the books next to each other on the shelf in the following cases: No two math books are next to each other.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52785)   (Show Source):
You can put this solution on YOUR website! .
On a library shelf there are 5 different science books and 4 different math books.
Find the number of ways to arrange the books next to each other on the shelf
if no two math books are next to each other.
~~~~~~~~~~~~~~~~~~~~~~
With 5 Science book on the bookshelf, we have 4 + 1 + 1 = 6 possible positions for the Math books
(4 positions between the Science books, one position on the left and one position on the right).
So, the number of all different placements of 4 different Math books is
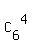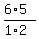 =  = 3*5 = 15.
We should multiply it by 5! = 120 (the number of permutations of 5 Science books)
and by 4! = 24 (the number of permutations of 4 Math books).
So, the final answer is 15*120*24 = 43200.
Solved.
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website!
First we'll arrange the books only subject-wise, as if the math books were
indistinguishable and the science books were also indistinguishable. Then we'll
rearrange (permute) them.
We start out with this configuration of all 5 math books with only 3 of the
science books separating them.
_ M S M S M S M _
I have underlined the 5 places we can put the other two science books. Each of
the three underlined S indicates that you can put one or both of them in with that
S, since science books can be placed together. The 2 empty underlines indicate
places where they can go as well, left or right of the others.
Case 1. You imagine "gluing" the 2 science books together and inserting the
"glued pair" in one of those 5 underlined places. That's 5 ways.
Case 2. You pick 2 separate underlined places to put them separately in. That's
C(5,2)=10 more ways.
So altogether, there would be only 5+10=15 ways to arrange them if the math
books were indistinguishable, and the science books were also indistinguishable.
But since none are indistinguishable books, we multiply by 5! to permute the
science books and by 4! to permute the math books.
Answer (15)(5!)(4!) = (15)(120)(24) = 43200 ways.
Edwin
|
|
|
