Question 1206897: Winning the jackpot in a particular lottery requires that you select the correct three numbers between 1 and 64 and, in a separate drawing, you must also select the correct single number between 1 and 27. Find the probability of winning the jackpot.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website!
there are 64 numbers between 1 and 64.
there are 27 numbers between 1 and 27.
the probability of getting 3 correct numbers between 1 and 64 is 1/64 * 1/64 * 1/64.
the probability of getting 1 correct number between 1 and 27 is 1/27.
the probability of getting 3 correct numbers between 1 and 64 and 1 correct number between 1 and 27 is 1/64 * 1/64 * 1/64 * 1/27.
that probability is equal to 1 / 7,077,888.
that's what it is, if i analyzed it correctly.
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In Math problems on lotteries, it is traditionally assumed that
(1) the numbers on a ticket are different (no repeating),
and
(2) the order of numbers on a ticket does not matter to determine winning.
If follow to the tradition in this current problem, it should be stated in the
problem, that
+---------------------------------------------------------------------+
| tree integer numbers from 1 to 64 on a ticket are different |
| (no repeating) and the order of the three numbers on the ticket |
| does not matter. |
+---------------------------------------------------------------------+
Below is my solution to the problem in this formulation.
There are 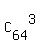 = = 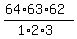 = 41664 different possible triples of numbers.
Combining it with the separate integer number from 1 to 27, we have, in all,
41554*27 = 1121958 possible outcomes (or tickets).
Only one of these tickets wins. So, the probability of winning is
P = 1/1,121,958 = = 41664 different possible triples of numbers.
Combining it with the separate integer number from 1 to 27, we have, in all,
41554*27 = 1121958 possible outcomes (or tickets).
Only one of these tickets wins. So, the probability of winning is
P = 1/1,121,958 = 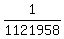 = 8.91299E-07.
It is a standard pattern of analysing/solving traditional Math problerms on lotteries.
As you see, the analysis and my answer are significantly different from that by @Theo. = 8.91299E-07.
It is a standard pattern of analysing/solving traditional Math problerms on lotteries.
As you see, the analysis and my answer are significantly different from that by @Theo.
Solved.
===================
My opinion is that, as a Math problem, this post must be worded differently,
to reflect all features of a lottery in explicit form.
|
|
|