SOLUTION: (a) How many different ways can 2 letters from the word SELECT be arranged? (b) How many different ways can 3 letters from the word SELECT be arranged?

Click here to see ALL problems on Permutations

Question 1206342: (a) How many different ways can 2 letters from the word SELECT be arranged?
(b) How many different ways can 3 letters from the word SELECT be arranged?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52780) (Show Source):
You can put this solution on YOUR website!
.
(a) How many different ways can 2 letters from the word SELECT be arranged?
(b) How many different ways can 3 letters from the word SELECT be arranged?
~~~~~~~~~~~~~~~~~~

Part (a) In the word SELECT, there are 5 different letters S, E, L, C, T, and one letter, E, is repeated twice. The word "arranged" means considering distinguishable permutations. So, consider the word SELCT. It has 5 unique letters (with no repeating). The number of all possible permutations of its two letters is 5*4 = 20. All these pairs are distinguishable. To it, we need to add one pair EE, and then these 21 = 20+1 pairs will present all possible distinguishable pairs. ANSWER to (a) : 21 different distinguishable pairs, or 21 different ways. Part (b) To solve (b), I will follow the similar logic. First, the number of all different triples, constituted of 5 different letters without repetitions, is 5*4*3 = 60. The number of all different triples, constituted of two E and any one of remaining 4 letters is 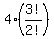= = 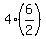4*3 = 12. To get the total number of all distinguishable triples, we should add 60 and 12. ANSWER to (b)) : 72 different distinguishable triples, or 72 different ways.

Solved.

Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!

Answers:
(a) 21
(b) 72

--------------------------------------------------------------------------
--------------------------------------------------------------------------

Explanation for part (a)

Break things up into three cases:
(1) Exactly zero 'E's are chosen
(2) Exactly one 'E' is chosen
(3) Exactly two 'E's are chosen

Case (1)
The letters to pick from are {S,L,C,T}
There are 4*3 = 12 different two letter words possible where "E" isn't chosen.
Alternatively, you can use the nPr permutation formula with n = 4 and r = 2.
Of course when I say "word", I mean it in quotes because much of these two-letter strings aren't words found in the dictionary.
An example word of case (1) would be SL.

Case (2)
Let's say "E" is in the first slot. There would be 4 words we can form which are: ES, EL, EC, ET
We will also have 4 words with "E" in the second slot.
That's 4+4 = 8 different words that have exactly one "E".
An example word of case (2) would be SE.

Case (3)
This is a trivial case of just one possibility. The word EE.

Add up the results:
12+8+1 = 21 is the final answer to part (a)

Here is the list of all 21 unique entries (7 rows, 3 columns)

1 SE SL SC
2 ST ES EL
3 EE EC ET
4 LS LE LC
5 LT CS CE
6 CL CT TS
7 TE TL TC

The list was generated using this combinatorics calculator
https://www.mathsisfun.com/combinatorics/combinations-permutations-calculator.html

--------------------------------------------------------------------------

Explanation for part (b)

We'll have three cases:
Case (1): Exactly 0 'E's are chosen
Case (2): Exactly 1 'E' is chosen
Case (3): Exactly 2 'E's are chosen
We stop here since we cannot select 3 "E"s.

Case (1)
There are 4 items to pick from in the set {S,L,C,T}
That gives 4*3*2 = 24 ways to form a three-letter word without any "E"s in it.
An example word of case (1) would be SLC.

Case (2)
We have 3 places to put the "E".
Then we have 4*3 = 12 ways to pick the other letters where order matters.
3*12 = 36 ways to form a three-letter word with exactly one "E" in it.
An example word of case (2) would be SEL.

Case (3)
There are 3 slots to choose from for one of these letters {S,L,C,T}
3*4 = 12 ways to form a three-letter word with exactly two "E"s in it.
An example word of case (3) would be SEE.

Add up the results:
24+36+12 = 72 is the final answer to part (b)

Below is the list of all 72 unique entries.
The list was generated with the previously mentioned link.
The table has 9 rows and 8 columns.

1 2 3 4 5 6 7 8
1 SEL SEE SEC SET SLE SLC SLT SCE
2 SCL SCT STE STL STC ESL ESE ESC
3 EST ELS ELE ELC ELT EES EEL EEC
4 EET ECS ECL ECE ECT ETS ETL ETE
5 ETC LSE LSC LST LES LEE LEC LET
6 LCS LCE LCT LTS LTE LTC CSE CSL
7 CST CES CEL CEE CET CLS CLE CLT
8 CTS CTE CTL TSE TSL TSC TES TEL
9 TEE TEC TLS TLE TLC TCS TCE TCL