Question 1206209:
How many 3 digit all even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many 3 digit all even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
~~~~~~~~~~~~~~~~~~~~~~
In the units position, only even digits 2, 4, 6 can be placed,
giving three different possible options.
In the tens and hundreds positions all of 6 given digits can be placed, independently,
giving 6*6 = 36 possible options.
In all, 6*6*3 = 36*3 = 108 different three-digit numbers are possible, having the assigned form.
Another way to solve is to notice that, in all, 6*6*6 = 216 three-digits numbers are possible,
and precisely half of them are even numbers.
It leads us to the same answer 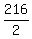 = 108. = 108.
Solved in two different ways, for your better understanding.
|
|
|