Question 1205063: You were tasked to program an algorithm for a number generator. The generator will be used by a soda company for their bottlecaps. The soda company will be holding a bottlecap lottery where 5 select bottlecaps will be winning combinations. There would be three characters printed on the bottlecaps with each character having the chance to be repeated. If a second person was to join, how many bottles of Pepsi will the 2nd person need to buy to have a 1% chance at winning.
Found 2 solutions by textot, ikleyn:
Answer by textot(100)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Determine the Total Possible Combinations**
* Since there are 3 characters and each character can be repeated, the total number of possible combinations on a bottlecap is 3 * 3 * 3 = 27.
**2. Probability of Winning for the First Person**
* The first person needs to find 5 specific winning combinations out of 27 possible combinations.
* The probability of winning for the first person on any given bottlecap is 5/27.
**3. Probability of Losing for the First Person**
* The probability of losing for the first person on any given bottlecap is 1 - (5/27) = 22/27.
**4. Probability of Losing Consecutively for the Second Person**
* Let 'n' be the number of bottles the second person needs to buy.
* The probability of losing 'n' consecutive times is (22/27)^n.
**5. Determine the Number of Bottles for a 1% Chance of Winning**
* We want the probability of losing consecutively to be 99% (100% - 1%):
* (22/27)^n = 0.99
* Solve for 'n':
* n = log(0.99) / log(22/27)
* n ≈ 0.45 / -0.1823
* n ≈ 2.47
* Since the second person can't buy a fraction of a bottle, they would need to buy **at least 3 bottles** to have a 1% chance of winning.
**Therefore, the second person needs to buy at least 3 bottles of soda to have a 1% chance of winning.**
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You were tasked to program an algorithm for a number generator. The generator will be used
by a soda company for their bottlecaps. The soda company will be holding a bottlecap lottery
where 5 select bottlecaps will be winning combinations. There would be three characters printed
on the bottlecaps with each character having the chance to be repeated. If a second person
was to join, how many bottles of Pepsi will the 2nd person need to buy to have a 1% chance at winning.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
To me, the way how this problem is worded in the post, is soup of words without clear meaning
(total gibberish, in plain English), as well as the solution, given to it in the post by other tutor.
Regarding the problem's formulation, I do not understand what the first person is doing
in this problem. I also do not understand what the generator of numbers is doing in this problem
and for what reason they tell me about it. From the problem, I do not understand what characters
do they use.
Regarding the solution by the other tutor, I do not understand which characters does he consider (uses),
how the other tutor interprets the second person's actions, why he consider how many losing are made.
So, as given, the problem is a fog and can not be considered as a Math problem.
Nevertheless, if to re-formulate this problem totally/radically/cardinally, it is possible to get really
interesting mathematical problem. I will make this editing right here step by step, then will solve
the updated/re-modeled problem.
First, I will take off a person named "You" with his algorithm as an unnecessary item (first sentence).
Second, I will remove every mention about this generator, together with the second sentence.
Now the problem's formulation will be as follows
The soda company will be holding a bottlecap lottery. In each bottlecap,
they will print 3 digits from 0 to 9 inclusive, allowing each digit
to be repeated. Some combination of 5 selected bottlecaps will be winning.
If a person wants to participate in this lottery, how many bottles of Pepsi
needs he to buy to have a 1% chance of winning.
Now it is 100% perfect, clean and clear Math problem, and my solution is below.
In this problem, the number of all possible different 3-digit numbers on bottlecaps is 10*10*10 = 1000.
It means that 1000 bottles/bottlecaps are in the game.
The number of all possible combinations of 1000 bottlecaps taken 5 at a time is 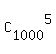 (the order does not matter). It is the gross pool of all possible combinations.
One of these combinations is winning.
Let n be the minimal number of bottles for the person to buy in order for to have a pool of combinations
(the order does not matter). It is the gross pool of all possible combinations.
One of these combinations is winning.
Let n be the minimal number of bottles for the person to buy in order for to have a pool of combinations
 , which is 0.01 of the gross pool , which is 0.01 of the gross pool 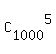 .
In other words, we want to solve this equation for n .
In other words, we want to solve this equation for n
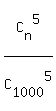 = 0.01. (1)
It is difficult to solve this equation directly (if possible, at all).
But it is possible to ESTIMATE "n", using well known asymptotic formulas for = 0.01. (1)
It is difficult to solve this equation directly (if possible, at all).
But it is possible to ESTIMATE "n", using well known asymptotic formulas for 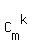 .
For great values of "m" and limited values of "k", the following asymptotic formula is valid .
For great values of "m" and limited values of "k", the following asymptotic formula is valid
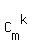 = = 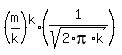 . (*)
If to use this formula in equation (1), it gives . (*)
If to use this formula in equation (1), it gives
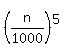 = 0.01.
Simplify it = 0.01.
Simplify it
 = = 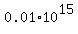 , ,
 = = 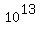 ,
n = 10^(13/5) = 398.1072.
So, this estimation tells that the number of bottles to buy for the person wishing
1% chance to win is 398, or about 400.
At this point the problem is solved completely to that extent
as the elementary probability methods allow to do it. ,
n = 10^(13/5) = 398.1072.
So, this estimation tells that the number of bottles to buy for the person wishing
1% chance to win is 398, or about 400.
At this point the problem is solved completely to that extent
as the elementary probability methods allow to do it.
Solved.
----------------------
Thus, what I did in this my post and what is my contribution, is listed here:
- I explained that the original formulation is total gibberish;
- I reformulated the problem and transformed it into the first class probability problem,
- and solved it to the end, providing first class solution.
/////////////////////////////
The reference to the formula (*) is this AI Overview
https://www.google.com/search?q=asymtotic+formula+for+C%5Bn%5D%5Ek+for+great+n&sca_esv=d2c0a33562fe64ea&rlz=1C1CHBF_enUS1071US1071&sxsrf=ADLYWIJjvf1rB_BUAXepFBBC4xLGziiRpg%3A1735105026743&ei=ApprZ_-FLb2d0PEPytqJaQ&ved=0ahUKEwj_jpH2mcKKAxW9DjQIHUptIg0Q4dUDCBI&uact=5&oq=asymtotic+formula+for+C%5Bn%5D%5Ek+for+great+n&gs_lp=Egxnd3Mtd2l6LXNlcnAiKGFzeW10b3RpYyBmb3JtdWxhIGZvciBDW25dXmsgZm9yIGdyZWF0IG4yCBAAGIAEGKIEMggQABiABBiiBDIIEAAYgAQYogQyCBAAGIAEGKIESJ0gUK8WWK8WcAF4AZABAJgBZ6ABZ6oBAzAuMbgBA8gBAPgBAZgCAqACccICChAAGLADGNYEGEeYAwDiAwUSATEgQIgGAZAGCJIHAzEuMaAH1QQ&sclient=gws-wiz-serp
|
|
|