Question 1204889: A boy has 7 red , 2 yellow and 5 green marbles. In how many ways can the boy arrange the marbles in a line if:
b) All marbles have different sizes?
c) Marbles of the same color are indistinguishable?
I'd need both parts solved pls.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers:
(b) 87,178,291,200
(c) 72,072
Explanation for part (b)
We have 7 red + 2 yellow + 5 green = 14 marbles total.
There are 14 choices for the 1st slot, then 13 choices for the next slot, and so on.
14! = 14*13*12*11*10*9*8*7*6*5*4*3*2*1 = 87,178,291,200
The exclamation mark represents factorial.
This value is a bit over 87 billion.
When converting to scientific notation, we get the approximate value 8.718 * 10^10
Another way to reach this value is to use the nPr permutation formula with n = 14 and r = 14.
Explanation for part (c)
In the previous part, we could tell marbles of the same color apart.
But now we have 7 red we cannot tell apart, and 2 yellow we cannot tell apart, and also 5 green we cannot tell apart.
For each group where we cannot tell them apart, we must divide by the factorial 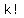 where k is the number of items in that group. where k is the number of items in that group.
For the reds we divide by 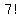
For the yellows we divide by 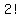
For the greens we divide by 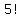
So,

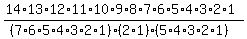
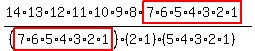
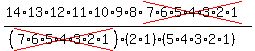
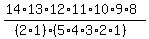
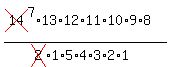
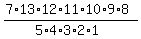
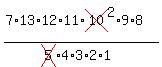

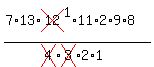
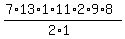


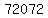
Your steps do not need to be as verbose. A calculator can make quick work of this.
In short,

There are 72,072 marble arrangements possible if we cannot distinguish the same color marbles from one another.
|
|
|