Question 1204860: 11 books are to be stored in a shelf where 4 books can be put vertically, so they are all as easily accessible, and 6 books can be piled-up, so the most used ones are on the top.
(a) In how many ways the books can be put in vertical positions?
Your answer is :
(b) In how many ways the books can be piled-up?
Your answer is :
(c) In how many ways the books can be put in both positions?
Your answer is :
out of 11 books only 10 will be on the shelf.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! ..
11 books are to be stored in a shelf where 4 books can be put vertically, so they are all
as easily accessible, and 6 books can be piled-up, so the most used ones are on the top.
(a) In how many ways the books can be put in vertical positions?
Your answer is :
(b) In how many ways the books can be piled-up?
Your answer is :
(c) In how many ways the books can be put in both positions?
Your answer is :
out of 11 books only 10 will be on the shelf.
~~~~~~~~~~~~~~~~~~
After thinking and re-finking, I came to another interpretation and changed my previous solution.
For clarity, I deleted that previous solution, and now you see my final updated version.
In this post, I solve the problem for question (c), ONLY.
According to the condition, 4 books on the shelf, that are stored vertically, should be considered
as unordered set. They all are "equally/easily accessible", so ordering does not matter for these 4 books.
For the set of 6 books, that are stored horizontally, there is ONLY ONE ordering "the most used ones are on the top".
Therefore, the combinatorial mechanism works as follows:
(1) First, we select 4 arbitrary books from 11 books and store them vertically on the left side of the shelf,
without looking on their order. It can be done in 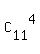 = 330 different ways
(classic combinations).
(2) Next, we select 6 books from remaining 11-4 = 7 books, and store them horizontally on the right side of the shelf.
For this set of 6 books, there is only one ordering according this criterion
"the most used ones are on the top". 6 books from 7 can be selected in = 330 different ways
(classic combinations).
(2) Next, we select 6 books from remaining 11-4 = 7 books, and store them horizontally on the right side of the shelf.
For this set of 6 books, there is only one ordering according this criterion
"the most used ones are on the top". 6 books from 7 can be selected in 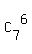 = 7 different ways
(classic combinations).
+-----------------------------------------+
| Half of the problem is just solved. |
| Now we will solve the second half. |
+-----------------------------------------+
(3) This time, we select 6 books from 11 books and store them horizontally on the left side of the shelf.
For this set of 6 books, there is only one ordering according this criterion
"the most used ones are on the top". 6 books from 11 can be selected in = 7 different ways
(classic combinations).
+-----------------------------------------+
| Half of the problem is just solved. |
| Now we will solve the second half. |
+-----------------------------------------+
(3) This time, we select 6 books from 11 books and store them horizontally on the left side of the shelf.
For this set of 6 books, there is only one ordering according this criterion
"the most used ones are on the top". 6 books from 11 can be selected in 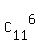 = 462 different ways
(classic combinations).
(4) Finally, we select 4 books from remaining 11-6 = 5 books, and store them vertically on the right side of the shelf,
without looking on their order ("they all are easily/equally accessible").
4 books from 5 can be selected in = 462 different ways
(classic combinations).
(4) Finally, we select 4 books from remaining 11-6 = 5 books, and store them vertically on the right side of the shelf,
without looking on their order ("they all are easily/equally accessible").
4 books from 5 can be selected in 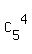 = 5 different ways
(classic combinations).
(5) The answer to the problems question (c) is 330*7 + 462*5 = 2310 + 2310 = 4620.
(6) Notice an interesting fact: the numbers of placing "vertical books on the left", 2310,
is the same as the number of placing "vertical books on the right", precisely as it should be due to symmetry. = 5 different ways
(classic combinations).
(5) The answer to the problems question (c) is 330*7 + 462*5 = 2310 + 2310 = 4620.
(6) Notice an interesting fact: the numbers of placing "vertical books on the left", 2310,
is the same as the number of placing "vertical books on the right", precisely as it should be due to symmetry.
Solved.
The key to the solution is to find / (to guess) right interpretation to written words,
which (interpretation) almost certainly is not clear explicitly and almost certainly is not unique.
So, my impression from this problem is two-fold.
From one side, the problem is original: I did not see such combinatorial problems with two "dynamic" subsets,
of which one is considered as unordered set, while the other has only one unique ordering.
From the other side, in this problem, very much depends on interpretation of words,
which (interpretation) is not unique.
So, as a conclusion, it is not a pure Math problem (they do not allow different interpretations).
Due to this reason, it is partly a puzzle type problem.
I would say that it needs further polishing to make it clean and clear Math problem.
If you could make it, you will get a brilliant (with my help).
=========================
Comment from student: I'm still having difficulty understanding question number 3.
The wording for this question is very odd which makes it not clear to understand certain things.
1) Does the order matter, for part a it seems like it does not and part b it mentions they want the most used books on top, meaning order matters?
2) Does the question want us to put the vertical books up and then get the combination to find the ways to pile them up,
vise versa or do we need to find the ways to put them up considering nothing has been put up yet?
My response : I got your message. It includes many questions and assumes detailed discussion each of them.
I do not want very much to make a mess at this spot. Therefore, I propose such strategy.
You will post your questions to the forum saying "for @ikleyn attention".
When I see it, I will answer step by step, question by question,
Then we will move forward without making a mess.
I will create my file in my archive, where I will keep the links to our posts,
and I advise to you to make your own file in your archive for easy navigation.
Doing this way, I think, we will be able to make a progress.
Here I will try to answer your question 1).
There are two basic options:
1a) We can consider the set of 4 vertical books as ordered, which means "the order does matter and books are easily (equally ?) accessible".
1b) We can consider 4 vertical books are unordered set, which means "order does not matter and all books are easily (equally ?) accessible".
Which of these two interpretations to take - it is entirely on the problem's creator decision,
they both have equal rights to exist; but it should be consistent with the wording MOTIVATION around it.
Otherwise, for what reason we need this ~motivation and pronounce the words ?
The ordering of 6 horizontal books is defined by an unique way: it is ordered
by an unique way according to the criterion "most used ones are on the top",
and there is NOTHING to discuss here.
So, the only "degree of freedom" is the choice between (1a) and (1b).
It is what I have to say regarding your first question.
For me, it is very important that we get agreement and common understanding with this basic issue before we will move further.
So, in your next post to me, please, let me know, if you understand everything in my writing to your question 1),
and do you agree and do you understand everything in full in it.
Then collect 1-2 your next questions, and we will move forward.
If your questions will repeat yours #2, #3 and so on, it does not stretch me.
I only want that as we move forward, there are no unclear questions left behind our backs.
Best regards.
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The wording of your post leaves open the possibility of very different interpretations of the problem.
(a) 4 books on the shelf vertically can be arranged in 4! = 24 different ways.
(b) 6 books in a pile can be arranged in 6! = 720 different ways.
(c) The 10 books together, 4 vertically and 6 in a pile, can be arranged in 24*720 = 17280 different ways.
If the intended problem involves which of the 11 books are stored vertically or in the pile, then of course that is a completely different problem.
If my answers are not what you expected, then re-post the problem, defining it clearly....
|
|
|