Question 1204818: A store is selling 7 types of hard candies: cherry, strawberry, orange, pineapple, apricot, blackberry, and lemon.
How many ways are there to choose:
(a) 17 candies?
Answer =
(b) 17 candies with at least a piece of each flavor?
Answer =
(c) 17 candies with at least 2 cherry and at least 3 lemon?
Answer =
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A store is selling 7 types of hard candies: cherry, strawberry, orange, pineapple, apricot, blackberry, and lemon.
How many ways are there to choose:
(a) 17 candies?
(b) 17 candies with at least a piece of each flavor?
(c) 17 candies with at least 2 cherry and at least 3 lemon?
~~~~~~~~~~~~~~~~~~~~
In this my post, I will solve parts (a) and (b), ONLY.
(a) In this problem, there are 7 boxes in the store, marked cherry, strawberry, orange, pineapple, apricot, blackberry, and lemon.
We take each kind of candies from the respective box. In this part (a), it is allowed do not take candies from some boxes.
So, we take n= 17 candies from k= 7 boxes according to their names and allowing to skip some boxes.
We want to know in how many different ways it is possible to collect 17 candies doing this way.
Notice that we distinct the candies only by their names. The boxes are different, since they carry different names.
Different collections of 17 selected candies distinct only by the number of identical candies of each kind.
It is a typical problem for "stars and bars" methodology. There is a general formula for the number of distinct selections
of this kind
N = 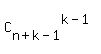 = = 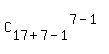 = = 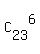 = = 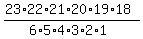 = 100947.
ANSWER. The number of distinct ways to select 17 candies in this problem (part (a) ) is 100947.
(b) This problem is very similar to part (a), but there is one VERY important difference:
+-------------------------------------------------------------+
| We MUST take at least one candy from each of 7 boxes; |
| it is NOT ALLOWED to skip any of boxes. |
+-------------------------------------------------------------+
Again, it is a typical problem for "stars and bars" methodology, but of the different kind.
There is a general formula for the number of distinct selections of this specific kind
N = = 100947.
ANSWER. The number of distinct ways to select 17 candies in this problem (part (a) ) is 100947.
(b) This problem is very similar to part (a), but there is one VERY important difference:
+-------------------------------------------------------------+
| We MUST take at least one candy from each of 7 boxes; |
| it is NOT ALLOWED to skip any of boxes. |
+-------------------------------------------------------------+
Again, it is a typical problem for "stars and bars" methodology, but of the different kind.
There is a general formula for the number of distinct selections of this specific kind
N = 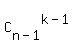 = = 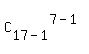 = =  = = 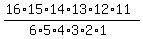 = 8008.
ANSWER. The number of distinct ways to select 17 candies in this problem (part (b) ) is 8008. = 8008.
ANSWER. The number of distinct ways to select 17 candies in this problem (part (b) ) is 8008.
Parts (a) and (b) are completed.
-------------------------
For the stars and bars method see this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_%28combinatorics%29
See also the lesson
- Stars and bars method for Combinatorics problems
in this site.
Learn the subject from there.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This kind of problem is one for which the "stars and bars" method is especially well suited.
Here is a simple example of this method.
Suppose we have 5 pieces of candy to be divided among 3 children.
Represent the pieces of candy with 5 stars:
* * * * *
To represent dividing the candy among 3 children, insert 2 bars in the string of stars.
*|* *|* *
Notice that to divide the candies among THREE children we need only TWO dividers.
Every different placement of the two dividers represents one of the distinct ways of dividing the 5 candies among the 3 children.
So the number of ways of dividing the 5 candies among the 3 children is the number of distinct ways of arranging the symbols *****||.
By a well-known counting principle, that number of ways is 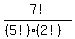 , or , or 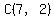 . .
Now to use this method on your problem....
(a) 17 candies, 7 different kinds --> 17 stars, 6 bars
ANSWER: 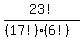 or or 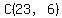 = 100947 = 100947
(b) 17 candies with at least a piece of each flavor
To use stars and bars for this problem, first select one piece of candy of each of the 7 kinds; that ensures that there will be one of each kind. Then there are 10 pieces of candy to be selected, with no further restriction on the number of each kind, so stars and bars can be used.
10 candies, 7 different kinds --> 10 stars, 6 bars
ANSWER: 
(c) 17 candies with at least 2 cherry and at least 3 lemon
Similar to (b), start by selecting the required 2 cherry and 3 lemon. That means 12 more candies to be selected, with no further restrictions on the number of each kind.
12 candies, 7 different kinds --> 12 stars, 6 bars
ANSWER: 
|
|
|